Примеры решения задач «Логические функции»

Примеры решения задач «Логические функции»

№1.

Запишите в виде логической формулы следующие высказывания:

1.      Если Иванов здоров и богат, то он здоров.

2.      Число является простым, если оно делится только на единицу и само на себя.

Решение:

1.Нам дано сложное составное высказывание. Выделим из него простые высказывания:

А = «Иванов здоров»

В = «Иванов богат»

Запишем высказывание в виде логической формулы A/\B=>A

2. Нам дано сложное составное высказывание. Выделим из него простые высказывания:

А = «Число является простым»

В = «Число делится только на единицу»

С=«Число делится на само себя»

Запишем высказывание в виде логической формулы  B/\C=>A

 

№2.

Для какого имени истинно высказывание:

¬ (Первая буква имени гласная  => Четвертая буква имени согласная)?

  1) Елена       2) Вадим       3) Антон        4) Федор

Решение:

  

 

 

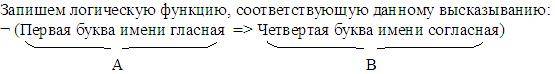
F(A, B) =  ¬ (A=> B)

По условию задачи функция F(A, B) истинна, следовательно, отрицание этой функции – ложно, т.е. высказывание (A=>B) – ложно. Полученное высказывание является импликацией и ложно только в том случае, когда выражение А истинно, а В —  ложно (см. табл. истинности импликации). Следовательно, среди предложенных ответов следует искать тот, в котором первая буква имени гласная  и четвертая буква имени также гласная. Этому условию удовлетворяет только имя АНТОН.

Ответ: 3

№ 3.

    Для какого числа X истинно высказывание  X>1 /\ ((X<5) => (X<3))

 1)  1                 2) 2               3) 3             4) 4

Решение:

 

 

 

 

 

 

По условию задачи F(A, B) истинна, следовательно, выражения А и В тоже должны быть истинны (см.табл.истинности конъюнкции), т.е.                                                                                                                                                               

 

 

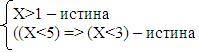
Рассмотрим предложенные ответы, подставляя значения Х в неравенства и проверяя истинность полученных высказываний:

Ответ 1): 1 > 1 – ложь, что противоречит первому условию;

Ответ 2): 2 > 1 – истина, первое условие совпадает,

(2<5) => (2<3), или (истина) => (истина), что является истиной (см. табл. истинности импликации). Т. е. второе условие также совпадает;

Ответ 3): 3 > 1 – истина, первое условие совпадает,

(3<5) => (3<3)  или (истина) => (ложь), что является ложью (см. табл. истинности импликации), это противоречит второму условию;

Ответ 4): 4 > 1 – истина, первое условие совпадает,

(4<5) => (4<3)  или (истина) => (ложь), что является ложью (см. табл. истинности импликации), это противоречит второму условию

Ответ: 2