Примеры решения логических задач
№1.
Кто из учеников Саша, Сергей, Дима и Андрей играет, а кто не играет в шахматы, если известно следующее:
а) если Саша и Сергей играет, то Дима не играет;
б) если Сергей не играет, то играют Дима и Андрей;
в) Дима играет?
Решение: Определим следующие простые высказывания:
А – «Саша играет в шахматы»;
В – «Сергей играет в шахматы»;
С – «Дима играет в шахматы»;
D – «Андрей играет в шахматы».
Запишем сложные высказывания, выражающие известные факты:
а) F1=(А \/ B) =>¬C;
б) F2=¬B => (С /\ D);
в) F3=C .
I способ: Запишем и упростим произведение указанных сложных высказываний:
((A \/ B) =>¬C) /\ (¬B => (С /\ D)) /\ С.
II способ: Составим таблицу истинности:
|
A |
B |
F3=C |
D |
¬C |
A \/B |
F1=(A \/B) =>¬C |
¬B |
С /\D |
F2=¬B => (С /\D) |
|
0 |
0 |
0 |
0 |
||||||
|
0 |
0 |
0 |
1 |
||||||
|
0 |
0 |
1 |
0 |
||||||
|
0 |
0 |
1 |
1 |
||||||
|
0 |
1 |
0 |
0 |
||||||
|
0 |
1 |
0 |
1 |
||||||
|
0 |
1 |
1 |
0 |
||||||
|
0 |
1 |
1 |
1 |
||||||
|
1 |
0 |
0 |
0 |
||||||
|
1 |
0 |
0 |
1 |
||||||
|
1 |
0 |
1 |
0 |
||||||
|
1 |
0 |
1 |
1 |
||||||
|
1 |
1 |
0 |
0 |
||||||
|
1 |
1 |
0 |
1 |
||||||
|
1 |
1 |
1 |
0 |
||||||
|
1 |
1 |
1 |
1 |
При F1 = F2 = F3 = 1 значения переменных соответствуют: А = 0, В = 0, С = 1, D = 1.
Ответ: в шахматы играют ученики Дима и Андрей, а Саша и Сергей – не играют.
№2.
«Ваза» Условие задачи:
Мама, прибежавшая на звон разбившейся вазы, застала всех трех своих сыновей в совершенно невинных позах: Саша, Ваня и Коля делали вид, что происшедшее к ним не относится. Однако футбольный мяч среди осколков явно говорил об обратном.
‑ Кто это сделал? ‑ спросила мама.
‑ Коля не бил по мячу, ‑ сказал Саша. ‑ Это сделал Ваня.
Ваня ответил: ‑ Разбил Коля, Саша не играл в футбол дома.
‑ Так я и знала, что вы друг на дружку сваливать будете, ‑ рассердилась мама. ‑ Ну, а ты что скажешь? ‑ спросила она Колю.
‑ Не сердись, мамочка! Я знаю, что Ваня не мог этого сделать. А я сегодня еще не сделал уроки, ‑ сказал Коля.
Оказалось, что один из мальчиков оба раза солгал, а двое в каждом из своих заявлений говорили правду.
Кто разбил вазу?
Решение (способ 1,алгебраический):
Обозначим высказывания:
А = «Коля разбил вазу»
В = «Ваня разбил вазу»
С = «Саша разбил вазу»
D = «Коля сегодня сделал уроки»
Согласно условию задачи, один из мальчиков солгал, а двое других говорили правду. Поэтому, если мы сложим записи истинного и ложного высказываний, составленных для каждого мальчика, то получим истинное высказывание.
Из слов Саши следует, что (¬А /\ B) \/ (А /\¬B) истинно;
Из слов Вани следует, что (А /\¬C) \/ (¬А /\ C) истинно;
Из слов Коли следует, что (¬В /\¬D) \/ (В /\ D) истинно.
Следовательно, истинна и конъюнкция
((¬А /\ B) \/ (А /\¬B)) /\ ((А /\¬C) \/ (¬А /\ C)) /\ ((¬В /\¬D) \/ (В /\ D)) = 1
Раскрывая скобки, получим:
((¬А /\ B) \/ (А /\¬B)) /\ ((А /\¬C) \/ (¬А /\ C)) /\ ((¬В /\¬D) \/ (В /\ D)) =
(¬AB \/A¬B) /\ (A¬C \/¬AC) /\ (¬B¬D \/ BD) = (A¬B¬C \/¬ABC) /\ (¬B¬D \/ BD) =
A¬B¬C¬B¬D \/¬ABC¬B¬D \/ A¬B¬CBD \/¬ABCBD = A¬B¬C¬D \/¬ABCD =
= A¬B¬C¬D = 1, следовательно, А=1. Т.е. Коля разбил вазу.
Ответ: Коля
Решение (способ логических рассуждений)
Предположим, что Саша сказал правду: Коля не разбивал вазу, вазу разбил Ваня. Из двух оставшихся мальчиков кто-то дважды солгал. Допустим, Ваня тоже сказал правду: Коля разбил вазу, Саша вазу не разбивал. Но это противоречит словам Саши. Тогда допустим, что Ваня дважды солгал. Тогда получается, что Коля не разбивал вазы, а вазу разбил Саша. Но это снова противоречит словам Саши. Следовательно, дважды солгал именно Саша, а Ваня и Коля говорили правду, т.е. вазу разбил Коля.
Ответ: Коля
№3.
Каждый ученик в классе изучает либо английский, либо французский язык, либо оба эти языка. Английский язык изучают 25 человек, французский — 27 человек, а то т и другой — 18 человек. Сколько всего учеников в классе?
Решение с помощью диаграмм Эйлера-Венна
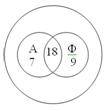
Английский язык изучают 7 учеников, французский — 9, и то т и другой 18, получаем, что всего в классе 7+9+18 = 34 ученика в классе.
Ответ: в классе 34 ученика.
№4.
«Сосуд» Условие задачи:
Алеша, Боря и Гриша нашли в земле сосуд. Рассматривая удивительную находку, каждый высказал по 2 предположения:
Алеша: «Этот сосуд греческий и изготовлен в V веке».
Боря: Этот сосуд финикийский и изготовлен в III веке».
Гриша: «Этот сосуд не греческий и изготовлен в IV веке».
Учитель истории сказал ребятам, что каждый из них прав только в одном из двух предположений.
Где и в каком веке изготовлен сосуд?
Решение:
При решении задач с помощью таблицы можно рассуждать так:
Пусть
Алеша: «Этот сосуд греческий и изготовлен в V веке» = А.
Боря: Этот сосуд финикийский и изготовлен в III веке» = Б.
Гриша: «Этот сосуд не греческий и изготовлен в IV веке» = Г.
|
3 век |
4 век |
5 век |
|
|
греческий |
А, Б |
А, Г |
|
|
финикийский |
Г |
Б |
А, Б, Г |
Вывод: сосуд финикийский изготовлен в 5 веке.
Ответ: сосуд финикийский изготовлен в 5 веке.
 МИР ЛОГИКИ
МИР ЛОГИКИ