Примеры решения задач «Логические выражения и таблица истинности»
Теория по этой теме по этой теме Пройти тестирование по этой теме Контрольная по этой теме
№1.
Докажите, что А <=> В равносильно (A\/ ¬B) /\ (¬A\/ B)
Для доказательства равносильности двух высказываний достаточно построить таблицу истинности для высказывания (A\/ ) /\ (\/ B) и сравнить ее с таблицей истинности эквивалентности:
|
А |
В |
¬B |
A\/¬B |
¬A |
¬AVB |
(A\/¬B) /\ (¬A \/B) |
|
0 |
0 |
1 |
1 |
1 |
1 |
1 |
|
0 |
1 |
0 |
0 |
1 |
1 |
0 |
|
1 |
0 |
1 |
1 |
0 |
0 |
0 |
|
1 |
1 |
0 |
1 |
0 |
1 |
1 |
Последние столбцы этих функций совпадают, значит, они равносильны. ЧТД.
№2.
Укажите, какое логическое выражение равносильно выражению
A /\ ¬ (¬B \/ C)
1) ¬A \/ ¬B \/ ¬C
2) A /\ ¬B /\ ¬C
3) A /\ B /\ ¬C
4) A /\ ¬B /\ C
Ответ: 3
№3.
Постройте таблицу истинности для логического выражения:
1)A=>B<=> ¬А \/ B
Ответ:
|
А |
В |
A=>B |
¬А |
A → B<=> ¬А |
A → B<=> ¬А \/ B |
|
0 |
0 |
1 |
1 |
1 |
1 |
|
0 |
1 |
1 |
0 |
0 |
1 |
|
1 |
0 |
0 |
0 |
1 |
1 |
|
1 |
1 |
1 |
0 |
0 |
1 |
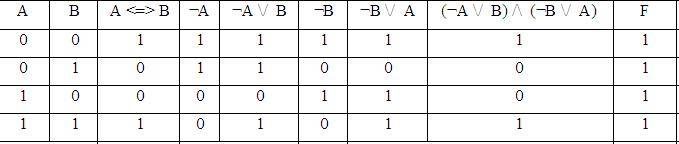
2)F=A<=>B<=>(¬А \/ B) /\ (¬B\/ А)
Ответ:
№4.
Определите истинность следующего высказывания: «За окном светит солнце, и нет дождя».
Решение:
Нам дано сложное составное высказывание. Выделим из него простые высказывания:
А = «За окном светит солнце»
В = «За окном дождь»
Составим логическую функцию, соответствующую данному высказыванию.
F(A, B) = A /\ ¬B
построим таблицу истинности для данной логической функции.
|
A |
B |
¬B |
A /\ ¬B |
|
0 |
0 |
1 |
0 |
|
0 |
1 |
0 |
0 |
|
1 |
0 |
1 |
1 |
|
1 |
1 |
0 |
0 |
Ответ: логическое выражение принимает значение истина только при наборе F(1,0)=1.Следовательно, данное нам высказывание истинно только тогда, когда первое простое высказывание истинно, а второе ложно.
№5.
Определите истинность следующего высказывания: «Гости смеялись, шутили и не расходились по домам».
Решение:
Выделим из данного сложного высказывания простые высказывания:
А = «Гости смеялись»
В = «Гости шутили»
С = «Гости расходились по домам»
Составим логическую функцию, соответствующую данному высказыванию.
F(A, B, С) = A/\ B /\¬C
Построим таблицу истинности для данной логической функции.
|
A |
B |
C |
¬C |
A /\ B/\¬C |
|
0 |
0 |
0 |
1 |
0 |
|
0 |
0 |
1 |
0 |
0 |
|
0 |
1 |
0 |
1 |
0 |
|
0 |
1 |
1 |
0 |
0 |
|
1 |
0 |
0 |
1 |
0 |
|
1 |
0 |
1 |
0 |
0 |
|
1 |
1 |
0 |
1 |
1 |
|
1 |
1 |
1 |
0 |
0 |
Ответ: логическое выражение принимает значение истина только при наборе F(1,1,0)=1.Следовательно, данное нам высказывание истинно только тогда, когда первое и второе простые высказывания истинны, а второе ложно.
№6.
На языке алгебры логики составьте истинное тождество, соответствующее заданному условию задачи:
Школьника, Миша, остававшийся в классе на перемене, был вызван к директору по поводу разбитого в это время окна в кабинете. На вопрос директора о том, кто это сделал, мальчик ответили следующее: «Я не бил окно, и Коля тоже…»
Известно, что он либо сказал чистую правду, либо в одной части заявления соврал, а другое его высказывание истинно, либо оба факта исказил.
Решение:
Пусть
А = «Окно разбил Миша»
В = «Окно разбил Коля»
Если Миша сказал чистую правду, то¬А /\ ¬В = 1.
Если в одной части заявления Миша соврал, а другое его высказывание истинно, то (¬А /\ В) \/ (А /\¬В) = 1
Если Миша оба факта исказил, то А /\ В = 1.
Ответ:
Истинное тождество, соответствующее условию задачи будет выглядеть так: ¬А /\ ¬В \/¬А /\ В \/А /\ ¬ В \/ А /\ В = 1.
 МИР ЛОГИКИ
МИР ЛОГИКИ