Алгебра высказываний
Высказывание – повествовательное предложение, о котором можно сказать истинно оно или ложно. В алгебре простым высказываниям ставятся в соответствии логические переменные (А, В, С и т.д.)
Логическая переменная – это простое высказывание.
Логические переменные обозначаются прописными и строчными латинскими буквами (a-z, A-Z) и могут принимать всего два значения – 1, если высказывание истинно, или 0, если высказывание ложно.
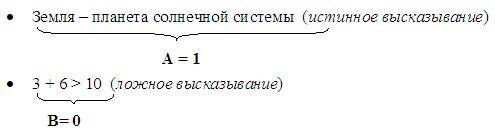
Для образования сложных высказываний наиболее часто используются базовые логические операции, выражаемые с помощью логических связок «и», «или», «не».
Например,
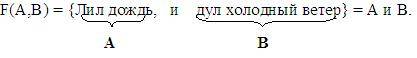
Многие люди не любят сырую погоду.
Пусть А = «Многие люди любят сырую погоду». Получаем логическую функцию F(A) = не А.
Связки «НЕ», «И», «ИЛИ» заменяются логическими операциями инверсия, конъюнкция, дизъюнкция. Это основные логические операции, при помощи которых можно записать любое логическое выражение.
Логическая формула (логическое выражение) — формула, содержащая лишь логические величины и знаки логических операций. Результатом вычисления логической формулы является ИСТИНА (1) или ЛОЖЬ (0).
Значение логической функции зависит от значений входящих в нее логических переменных. Поэтому значение логической функции можно определить с помощью специальной таблицы (таблицы истинности), в которой перечислены все возможные значения входящих логических переменных и соответствующие им значения функции.
1. Логическое умножение (конъюнкция), от лат. konjunctio – связываю:
• Объединение двух (или нескольких) высказываний в одно с помощью союза И;
• в языках программирования — And.
• Принятые обозначения: /\ , •, и, and.
• В алгебре множеств конъюнкции соответствует операция пересечения множеств.
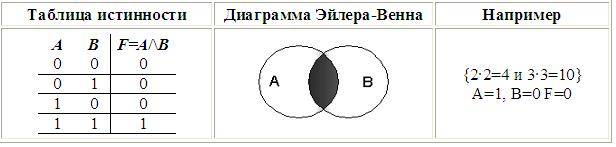
Пример:
Рассмотрим составное высказывание «2 • 2 = 4 и 3 • 3 = 10». Выделим простые высказывания:
А = «2 • 2 = 4» = 1 (т.к. это истинное высказывание)
В = «3 • 3 = 10» = 0 (т.к. это ложное высказывание)
Поэтому, логическая функция F(A, B) = A /\ B = 1 /\ 0 = 0 (в соответствии с таблицей истинности), то есть данное составное высказывание ложное.
2. Логическое сложение (дизъюнкция), от лат. disjunctio – различаю:
• Объединение двух (или нескольких) высказываний в одно с помощью союза ИЛИ;
• в языках программирования — Or.
• Обозначение: \/, +, или, or.
• В алгебре множеств дизъюнкции соответствует операция объединения множеств.
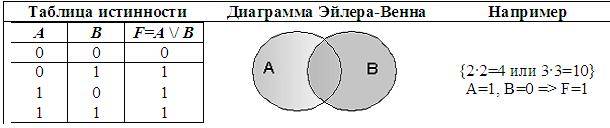
Пример:
Рассмотрим составное высказывание «2 • 2 = 4 или 2 • 2 = 5». Выделим простые выска-зывания:
А = «2 • 2 = 4» = 1 (т.к. это истинное высказывание)
В = «2 • 2 = 5» = 0 (т.к. это ложное высказывание)
Поэтому, логическая функция F(A, B) = A \/ B = 1 \/ 0 = 1 (в соответствии с таблицей истинности), то есть данное составное высказывание истинно.
3. Отрицание (инверсия), от лат. InVersion – переворачиваю:
• Соответствует частице НЕ, словосочетаниям НЕВЕРНО, ЧТО или НЕ ЯВЛЯЕТСЯ ИСТИНОЙ, ЧТО;
• в языках программирования — Not;
• Обозначение: не А, ¬А, not
• В алгебре множеств логическому отрицанию соответствует операция дополнения до универсального множества.
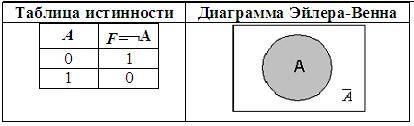
Пример:
А = {два умножить на два равно четырем} = 1.
¬A= {Неверно, что два умножить на два равно четырем}= 0.
Рассмотрим высказывание А : «Луна — спутник Земли«; тогда ¬А будет формулироваться так: «Луна — не спутник Земли«.
Рассмотрим высказывание: «Неверно, что 4 делится на 3». Обозначим через А простое высказывание «4 делится на 3». Тогда логическая форма отрицания этого высказывания имеет вид ¬А
Приоритет логических операций:
1. инверсия;
2. конъюнкция;
3. дизъюнкция;
Для изменения указанного порядка выполнения логических операций используются круглые скобки.
Составные логические выражения алгебры высказываний называют формулами.
Истинно или ложно значение формулы можно определить законами алгебры логики, не обращаясь к смыслу:
F = (0 \/ 1) /\ (¬0 \/ ¬1) = (0 \/ 1) /\ (1 \/ 0) =1 /\ 1=1 — истина
F = (¬0 /\ ¬1) \/ (¬1 \/ ¬1) = (1 /\ 0) \/ (0 \/ 0) = 0 \/ 0 = 0 — ложь
 МИР ЛОГИКИ
МИР ЛОГИКИ