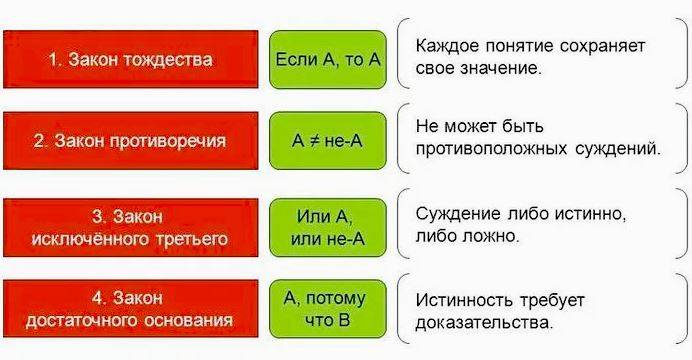
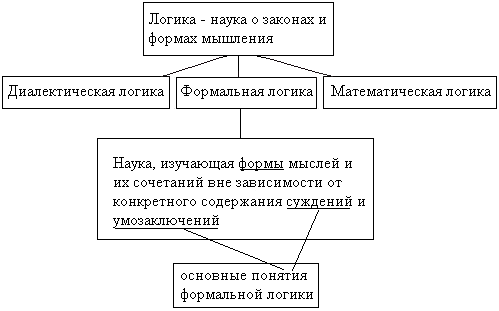
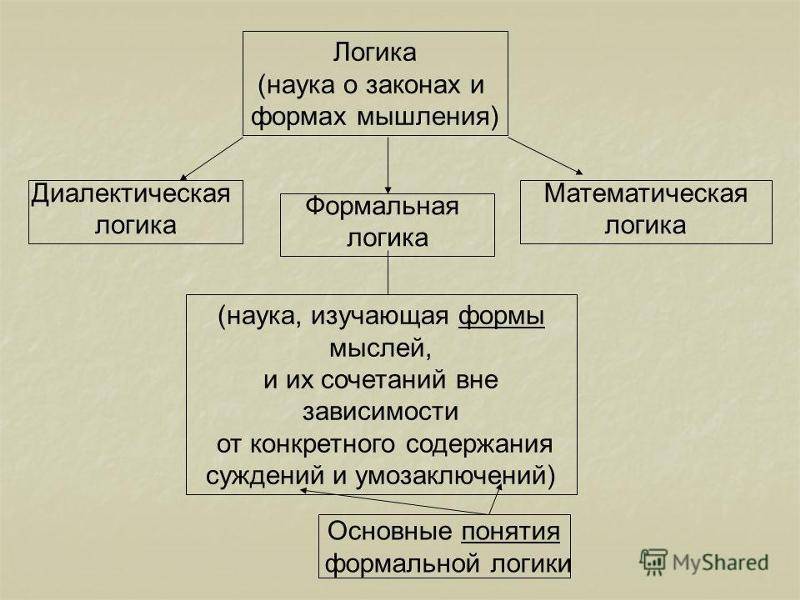
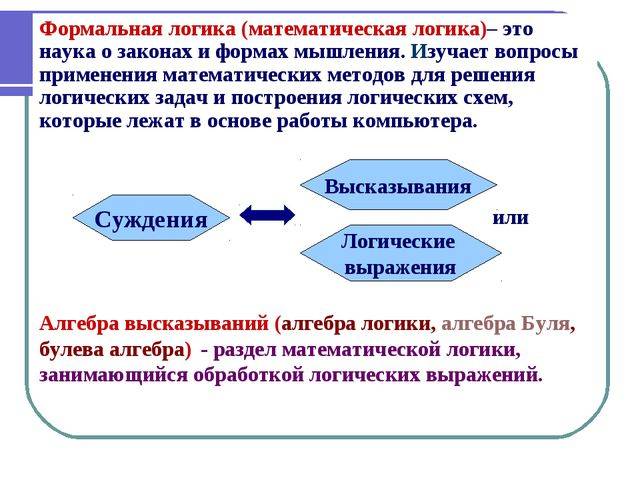
Задачи формальной логики
Введение
Наука логика – одна из древнейших наук. Ее следы просматриваются в древнеиндийской и древнекитайской философии, а также в философии античной Греции. Наиболее значительной фигурой здесь был Аристотель, которого по праву считают основателем формальной логики. В его сочинениях мы находим основы теоретического знания о формах и приемах мышления. В дальнейшем логика развивалась другими философами, которые видели в ней необходимую науку о мышлении, без которой невозможно успешное развитие познавательного процесса. Возникнув в рамках философии, логика вышла за ее пределы и стала необходимым инструментом мышления в науке, в политике, в экономике, в сфере общественной и культурной жизни, в повседневных делах самых широких слоев населения. Сегодня логика служит политику и юристу, ученому и студенту, бизнесмену и общественному деятелю, руководителю и исполнителю, домохозяйке и педагогу и т.п. Формально-логическое мышление обладает всеобщей обязательностью, и в этом состоит его сила. Почему? Что такое логика как наука?
Споры вокруг формальной логики в Советском Союзе
В 1930—1940-е годы формальная логика третировалась официальными философскими инстанциями как «теоретическая основа буржуазного мировоззрения», нечто несовместимое с марксизмом и коммунистическими идеалами. Активной работы в соответствующих направления не было, традиции были утрачены, немногие остававшиеся в живых специалисты были вынуждены заниматься другими дисциплинами или были лишены условий для нормального научного общения.
Ситуация несколько изменилась в — годах, когда (по некоторым сведениям, по личному распоряжению И. В. Сталина) логика была введена в состав школьной программы (был написан ряд учебников (В. Ф. Асмуса, К. С. Бакрадзе, М. С. Строговича) и даже в сокращенном или переработанном виде переизданы «буржуазные» учебники С. Н. Виноградова и Г. И. Челпанова). За этим последовало создание кафедры логики на Философском факультете Московского университета (в качестве одного из кандидатов на занятие кафедры рассматривался А. Ф. Лосев, хотя в конце концов занял её П. С. Попов), издание ряда книг по формально-логической тематике и некоторые другие мероприятия.
Однако вокруг этой тематики с переменным успехом продолжалась борьба «диалектиков» и «формалистов». В 1950—1960-е годы формальная логика (уже уйдя из школы) обосновалась в вузах и исследовательских институтах. Выдающуюся роль в восстановлении логических исследований и преподавания логики в стране сыграли такие представители формалистического направления, как С. А. Яновская, А. С. Есенин-Вольпин, Ю. А. Гастев, А. А. Марков и др.
Обратной стороной процесса стала контрреакция со стороны «формалистов» по отношению к логикам, стремившимся разрабатывать логику вне программы её формализации. Уже в 1960—1970-е годы сложности с публикациями испытывали такие логики, как А. А. Зиновьев (вынужденный затем сменить язык и перейти на «математические» символы), Э. В. Ильенков (покинувший коллектив «Философской энциклопедии» в знак протеста против подмены логической проблематики математической) и др.
До некоторой степени эта реакция продолжается даже в постсоветские годы.
Литература
Асмус В.Ф. Логика. – М., 1947
Войшвилло Е.К., Дегтярев М.Г. Логика. Учебник. – М., 2001.
Гетманова А.Д. Логика. Словарь и задачник. – М., 1998.
Маклаков А.Г. Общая психология – СПб., — 2001.
Общая психология. Учебник. \ Под ред. А.В.Петровского. – М., 1986.
Тоноян Л.Г. Сборник задач и упражнений по логике. – СПб., 2000.
Асмус В.Ф. Логика. – М., 1947
Войшвилло Е.К., Дегтярев М.Г. Логика. Учебник. – М., 2001.
Общая психология. Учебник. \ Под ред. А.В.Петровского. – М., 1986.
Маклаков А.Г. Общая психология – СПб., — 2001.
Тоноян Л.Г. Сборник задач и упражнений по логике. – СПб., 2000.
Асмус В.Ф. Логика. – М., 1947
Войшвилло Е.К., Дегтярев М.Г. Логика. Учебник. – М., 2001.
Асмус В.Ф. Логика. – М., 1947
Войшвилло Е.К., Дегтярев М.Г. Логика. Учебник. – М., 2001.
Формальная логика (ред. Чупахин И.Я., Бродский И.Н.)
Название: Формальная логика
Под редакцией: Чупахин И.Я., Бродский И.Н.
Ленинград: Издательство Ленинградского университета, 1977.- 357 с.DjVu 3,77 Мб
Качество: сканированные страницы, текстовый слой
Язык: Русский
В основу учебника положен курс логики, читавшийся на философском факультете Ленинградского университета в течение ряда лет. В нем освещаются вопросы, относящиеся к общей и символической логике. Учебник предназначен для студентов-философов и студентов других гуманитарных факультетов и педагогических вузов.
Введение 3 § 1. Марксистская философия о мышлении — § 2. Мышление и язык 4 § 3. Определение формальной логики 5 § 4. Логика и психология 9 § 5. Из истории логики 10 § 6. Практическое значение формальной логики 16 § 7. Структура формальной логики 19
Часть первая. ОБЩАЯ ЛОГИКА. ОСНОВНЫЕ ЛОГИЧЕСКИЕ ФОРМЫ И МЕТОДЫ МЫШЛЕНИЯ
Глава I. Понятие§ 8. Об определении и структуре понятия§ 9. Основные методы образования понятий§ 10. Соотношение между содержанием и объемом понятия§ 11. Виды понятий§ 12. Формально-логические отношения между понятиями по содержанию и по объему § 13. Обобщение и ограничение понятийГлава II. Суждение§ 14. Сущность суждения и его строение§ 15. Суждение и предложение § 16. Суждение и вопрос § 17. Деление суждений по качеству и количеству§ 18. Объединенная классификация суждений по качеству и количеству§ 19. Распределеиность терминов в категорических суждениях§ 20. Отношения между суждениями§ 21. Деление суждений по модальности§ 22. Сложные сужденияГлава III. Основные формально-логические законы§ 23. Обшие замечания § 24. Закон тождества§ 25. Закон противоречия§ 26. Закон исключенного третьего§ 27. Закон достаточного основания Глава IV. Умозаключение § 28. Определение умозаключения§ 29. Непосредственные умозаключения § 30. Простой категорический силлогизм § 31. Сокращенные, сложные и сложносокращенные категорические силлогизмы§ 32. Условные, разделительные и условно-разделительные силлогизмы§ 33. Индуктивные умозаключения § 34. АналогияГлава V. Логические методы научного мышления§ 35. Методы классификации объектов исследования§ 36. Определение§ 37. Доказательство§ 38. Доказательство (продолжение: паралогизмы, софизмы и парадоксы)§ 39. Аксиоматический метод§ 40. Индуктивные методы установления причинной связи явлений § 41. Гипотеза§ 42. Вероятностные методы в логикеЧасть вторая. СИМВОЛИЧЕСКАЯ ЛОГИКАГлава I. Табличное построение логики высказываний§ 1. Высказывания и формы высказываний§ 2. Язык логики высказываний§ 3. Семантика логических знаков§ 4. Таблицы формул логики высказываний§ 5. Равносильные формулы § 6. Правило равносильной замены § 7. Полные системы логических знаков§ 8. Закон двойственности§ 9. Тождественно-истинные и тождественно-ложные формулы Глава II. Нормальные формы формул логики высказываний§ 10. Нормальная форма§ 11. Проблема разрешения§ 12. Конъюнктивная нормальная форма и совершенная конъюнктивная нормальная форма§ 13. Логическое следование и логические следствия§ 14. Сокращенная конъюнктивная нормальная форма§ 15. Дизъюнктивные нормальные формыГлава III. Естественный вывод в логике высказываний§ 16. Понятия логического вывода§ 17. Производные правила§ 18. Чисто прямое доказательство§ 19. Слабое косвенное доказательство§ 20. Квазисильное косвенное доказательство§ 21. Сильное (классическое) косвенное доказательство§ 22. Полнота классического нечисления высказываний§ 23. Аксиоматическое представление логики высказыванийГлава IV. Формализованная силлогистикаГлава V. Естественный вывод в логике предикатовГлава VI. Модальная логика
-
Назад
-
Вперёд
Литература
- Кондаков Н. И. Логический словарь / Горский Д. П.. — М.: Наука, 1971. — 656 с.
- Arnold vander Nat. Simple formal logic: with common-sense symbolic techniques. — Routledge, 2010. — 360 с. — ISBN 978-0415997454.
- Чупахин И. Я., Бродский И. Н. Формальная логика. — Л.: ЛГУ, 1977. — 357 с.
История логики
- Маковельский А. О. История логики. — М., .
- Попов П. С. История логики нового времени. — М., .
- Logic, history of: Precursors of modern logic // Encyclopedia of philosophy / Donald M. Borchert, editor in chief. — 2nd ed. — N. Y.: Thomson Gale, 2006. — Т. 5. — С. 440—446. — 742 с. — ISBN 0-02-865785-3.
- Logic, history of: Modern logic // Encyclopedia of philosophy / Donald M. Borchert, editor in chief. — 2nd ed. — N. Y.: Thomson Gale, 2006. — Т. 5. — С. 447—484. — 742 с. — ISBN 0-02-865785-3.
Судьба формальной логики в СССР
- Алексеев М. Н. Обсуждение вопросов логики в Московском государственном университете // Вопросы философии, , № 2;
- Алексеев М. Н. Дискуссия по вопросу соотношения формальной логики и диалектики // Вестник МГУ, Серия I. Общественные науки, 1951, № 4.
- Щедровицкий Г. П. Я всегда был идеалистом…. — М., 2001. — 323 с. — ISBN 5-93733-010-2.
Суждения.
Суждение – мысль, посредством которой выделяется предмет, раскрывается часть его содержания и утверждается его отношение между предметом и выделенной частью его содержания.
Категорические суждения – множественные атрибутивные суждения
Логические типы суждений.
По логическому характеру отношения субъекта S и предиката Р суждения делятся на группы:
Группа 1. Отношение S и Р мыслится как принадлежность свойств предмету.
Группа 2. Отношение S и Р – как принадлежность предмета классу предметов.
Группа 3. Отношение S и Р — как отношение двух предметов по какому-либо признаку.
Качество суждений.
Утвердительная форма – соединение в действительности.
Отрицательное суждение – разъединение.
Количество суждений.
Общие суждения «все S-Р»;
Частное суждение «некоторое S-Р»;
Единичное суждение «это S-Р».
Виды суждений по отношению.
Категорические, без ограничения по условиям;
Условные, истинность состоит в зависимости от условий;
Разделительные, «А есть или В, или С, или Д».
Модальность суждений.
Аподиктические – выражают необходимость утверждения, обусловлены самим предикатом;
Проблематические – выражают вероятность и возможность противоположного утверждения.
Суждения одновременно по количеству и качеству:
Общеутвердительные – стандартная, логическая форма – «все S суть Р»;
Общеотрицательное — «ни одно S не есть Р»;
Частноутвердительное — «некоторые S суть Р»;
Частноотрицательные – «некоторые S не суть Р».
Преобразования формы суждений.
Преобразования формы суждений, операциями обращения, превращения, преобразования, производится посредством противопоставления предикату.
Превращение – это вывод, в котором заключение получается посредством эквивалентного преобразования утвердительного суждения в отрицательное и наоборот. Эквивалентность достигается за счет того, что при изменении качества суждения изменяется его предикат – он заменяется противоречащим понятием.
Обращение – это умозаключение, при котором из данного суждения, не являющегося частноотрицательным, выводится такое, субъектом которого является предикат исходного, а предикатом — субъект исходного, т.е. преобразование Р в S, S в Р, с сохранением логического содержания.
Противопоставление предикату – вывод последовательным применением превращением исходного суждения и далее обращением полученного суждения.
Утрата специфики
Распространение идей многозначной логики в различных её вариантах (в том числе, символизированных), а затем — идей абстрактных типов данных в теоретическом программировании проблематизировало «изнутри» специфику истинности как области значений логических функций, включающих лишь два возможных значения. Так, аппарат бесконечнозначной логики Лукасевича—Тарского практически неотличим от аппарата теории вероятностей, а в теории типов данных логический (булев) тип ничем особенным не отличается от прочих ни с операторной точки зрения, ни с точки зрения машинной реализации.
С другой стороны, новые разделы и версии символической логики (например, интуиционистская логика, интенциональная логика, деонтическая логика) вышли далеко за пределы силлогистики и исследования истинности в узком смысле и охватили собой многие другие разделы логики.
В настоящее время термин «формальная логика» утратил специфическое значение и применяется (вне контекста истории науки) как синоним символической, или математической логики. «Традиционной» (в противоположность «современной») формальной логикой могут называть те же разделы логики, изложенные без применения математического аппарата.
Суждение
Суждение (или высказывание) – это форма мышления, в которой что-либо утверждается или отрицается. Например:
- Если человек читает, значит, он знает буквы.
- Любой ребенок нуждается в матери.
- Все собаки – это не кошки.
- Многие цветы приятно пахнут.
Давайте рассмотрим основные свойства суждения, чтобы понять, чем оно отличается от понятия.
- Любое суждение состоит из связанных между собой понятий. Для примера возьмем два понятия – мужчина и женщина. Из них можно составить несколько суждений:
- мужчины и женщины – это люди;
- мужчины не являются женщинами;
- некоторые женщины сильнее мужчин.
- Любое суждение выражается в форме предложения (в то время как понятие выражается словом). При этом не каждое предложение обязательно должно быть суждением.
- Любое суждение является либо истинным, либо ложным. Если оно соответствует действительности, оно истинное, а если не соответствует – ложное.
- Суждения бывают простыми и сложными. Сложные суждения состоят из простых, соединенных каким-либо союзом.
Из всего вышесказанного вытекает, что суждение представляет собой гораздо более сложную форму логического мышления, чем понятие. Именно поэтому в суждении выделяют четыре части: субъект, предикат, связку и квантор.
Не пугайтесь этих слов, они вовсе не так сложны, как кажется на первый взгляд. Кратко рассмотрим их.
Субъект (S) – это то, о чем идет речь в суждении. В суждении «Все растения не животные» речь идет о растениях, поэтому в данном случае субъектом являются растения.
Предикат (Р) – это то, что говорится о субъекте. В том же суждении «Все растения не животные» о субъекте «растения» говорится, что они – «не животные», поэтому предикатом данного суждения выступает понятие «животные».
Связка – это то, что соединяет субъект и предикат. Роль связки могут выполнять самые разные слова: есть, является, находится, это и т. п.
Квантор – это указатель на объем субъекта. В роли квантора могут быть слова все, некоторые, каждый пятый, половина, ни один и т. п.
Для закрепления давайте проанализируем простое суждение «Многие школьники любят физкультуру».
- Субъект – «школьники»
- Предикат – «физкультура»
- Связка – «любят»
- Квантор – «многие»
Надеемся, что это понятно. Стоит также отметить, что в некоторых суждениях квантор может отсутствовать. Однако он обязательно подразумевается. В суждении «Бабочки – это насекомые» квантор видимым образом отсутствует, но он подразумевается – это слово «все».

Вопросы в логике
Теперь давайте разберемся с тем, что такое вопрос, и почему его правильность так важна для логики.
Дело в том, что сам по себе вопрос очень близок к суждению. По сути, вопрос – это логическая форма, направленная на получение ответа в виде суждения.
Любой вопрос состоит из двух частей:
- Основной (базисной), выраженной неким суждением (предпосылка вопроса);
- Искомой, указывающей на необходимость дополнения этого суждения каким-то ответом.
С точки зрения логики одним из основных требований к постановке вопроса является истинность суждения базисной части. В противном случае вопрос считается логически некорректным.
Например, вопрос: «В каком году Достоевский написал «Войну и мир»?» следует признать логически некорректным, так как его базисная часть выражена ложным суждением «Достоевский написал «Войну и мир»».
Программа «логистики»
Формалистами (представителями т. н. «логистики», оформившейся на Женевском конгрессе г. усилиями Л. Кутюра, А. Лаланда и др.) конца XIX — начала XX века формальность логики связывалась с выделением значений истинности высказываний при переносе их из естественного языка в символическую нотацию. Логистики стремились дать обоснование математическому знанию (в перспективе — естествознанию) в пределах одной только формальной логики. Существенные усилия в этом направлении были приложены Д. Гильбертом, Кутюра, Б. Расселом.
Фокус на истинностном значении отличал формальную логику от других дисциплин, имеющих дело с формой, как то: лингвистика и такие математические дисциплины, как арифметика, геометрия, алгебра, математический анализ. Соответственно, к формальной логике ими относились все те разделы логики, которые удалось формализовать в символических формах, разработанных в XIX—начале XX век математиками и логиками О. де Морганом, Дж. Булем, Дж. Пеано, Г. Фреге, Расселом и другими.
«За бортом» формальной логики оставались такие логические дисциплины, как диалектика (в её средневековой версии и различных нововременных вариантах), индуктивная логика (Дж. С. Милль) и другие варианты логики науки.
Так понимаемая формальная логика переставала быть наукой о мышлении, и многими формалистами последнее вовсе дезавуировалось как «психологическое» понятие, не имеющее отношения к логике как таковой, которая должна сосредоточиться на изучении и совершенствовании языка, на структурных, а не процессуальных свойствах речевых конструкций. Эта точка зрения нашла развитие во взглядах Венского кружка, Львовско-Варшавской школы и, далее, англосаксонской аналитической философии. Однако другими формалистами она не разделялась.
В то же время в 1910—20-х гг. претензии логистиков на обоснование точного знания убедительно критиковались А. Пуанкаре и, позднее, примкнувшим к нему в этой критике Гильбертом, после чего логистическое движение сошло на нет.
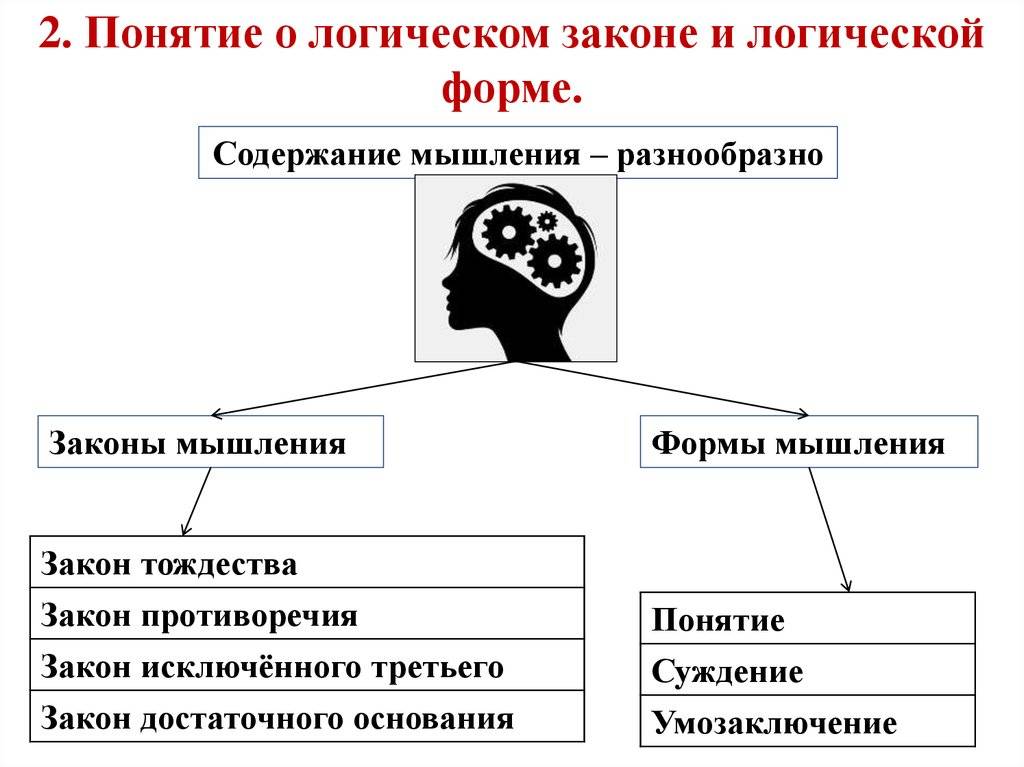
Формы мышления
Для обязательного понимания логики следует знать, что существует три основных формы мышления: понятие, суждение и умозаключение. Остановимся вкратце на каждой из них.
Понятие – это форма мышления, которая обозначает какой-либо объект или его признак. Например: стул, красота, улыбка, воздух, человек, совесть, космос, разумность, подарок.
Суждение – это форма мышления, которая состоит из связанных между собой понятий. Суждение обязательно что-нибудь утверждает или отрицает. Например: все звезды – это небесные тела, многие спортсмены имеют травмы, любая ручка не есть карандаш.
Умозаключение – это форма мышления, в которой из двух или нескольких исходных суждений (посылок) вытекает новое суждение (вывод).
Здесь стоит сделать важное отступление. Дело в том, что логика изучает не только формы мышления, но и занимается его законами
Тренинги
Тренировка и развитие логического мышления могут быть дополнены следующими тренингами, которые вы сможете бесплатно пройти на нашем сайте:
1
Память и внимание являются важными способностями для логического мышления, которые позволят концентрироваться на большом количестве мыслительных объектов, над которыми осуществляются логические операции
2. Творческое мышление вместе с логикой даст вам возможность не только строить правильные выводы, но искать нестандартные решения там, где логика «зашла в тупик».
3. Ораторское искусство и писательское мастерство формируют словестно-логическое мышление, а также позволяют на практике применить полученные знания в данном курсе.
4. Устный счет и скорочтение подходят для развития и тренировки интеллектуальных способностей.
5. Психология человека является полезной в понимании логического мышления, ведь именно психология как наука изучает мыслительные операции, мотивы, стимулы человека.
Понятие
Понятие – это форма мышления, которая обозначает какой-либо объект или его свойство. Приведем несколько случайных понятий:
- дерево
- улыбка
- телефон
- солнце
- молекула
- бутерброд
- красота
При этом можно подумать, что понятие и слово – это одно и то же. Ведь понятие ребенок мы выражаем словом ребенок. Тем не менее, понятие и слово – это разные вещи.
Понятие – это мысленное обозначение объекта (мысль о нем), а слово – это лишь языковое выражение этой мысли. Иными словами, понятие – это форма мышления, а слово – форма языка.
Понятие новорожденный для всех людей мира одно: оно обозначает недавно родившегося человека, а не стол, воздух или карандаш. Но словесное выражение этого понятия будет во всех языках разное.

Выполнение задания
9)Установите термины, входящие в состав данного сложного суждения и напишите его в символической форме, используя логические знаки конъюнкции, дизъюнкции, импликации и эквиваленции:
Характерной особенностью России является неравномерность освоения её территории. Процесс организации территориального управления всегда отличала неполная вовлеченность и иных природных и территориальных ресурсов в общий ресурсообмен, содержащий серьезные диспропорции.
В состав данного сложного суждения входят следующие термины:
ИМЕНА – Характерная особенность, Россия, неравномерность освоение, территория, процесс организации, природные и территориальные ресурсы, ресурсообмен, управление.
ПРЕДИКАТОРЫ – вовлеченность, иных, общий.
ПРЕДМЕТНЫЕ ФУНКТОРЫ – диспропорции, неравномерность, неполная.
ЛОГИЧЕСКИЕ КОНСТАНТЫ — и, всегда, содержащий, является.
ПРЕДЛОЖЕНИЯ – повествовательные.
Символическая форма суждения:
( a Ù b) ≡(c Ù (d Ú t)) É g
Примечания
- , p. 2.
- .
- , с. 576.
- Кант И. Критика чистого разума. — М.: 1994. — С. 14.
- Кант И. Цит. соч. — С. 72—73.
- Scholz H. Concise History of Logic. — New York, .
- Carnap R. Induktive Logik und Wahrscheinlichkeit. — Wien, 1958. — С. 31.
- Лукасевич Я. Аристолевская силлогистика с точки зрения современной формальной логики. — М., 1959. — С. 48—49.
- Пуанкаре А. О науке. — М.: Наука, 1983. — С. 475—518, 580—616. — 736 с.
-
Зиновьев А. А. Восхождение от абстрактного к конкретному (на материале «Капитала» К. Маркса). — М., 2002. — 321 с.;
;
;
;
Ладенко И. С. Об отношении эквивалентности и его роли в некоторых процессах мышления // Доклады АПН РСФСР. — 1958. — № 1.;
Ладенко И. С. О некоторых процессах мышления, связанных с установлением отношения эквивалентности // Доклады АПН РСФСР. — 1958. — № 2.
Швырёв В. С. К вопросу о путях логического исследования мышления // Доклады АПН РСФСР. — 1960. — № 2. и др. -
;
;
;
Щедровицкий Г. П. О взаимоотношении формальной логики и неопозитивистской «логики науки» // Диалектический материализм и современный позитивизм : Сб. — М., 1961.; - Щедровицкий Г. П. О методе исследования мышления. — М., 2006. — С. 110—183. — 600 с.. См. тж. и Щедровицкий Г. П. Проблемы логики научного исследования и анализ структуры науки / Из архива Г. П. Щедровицкого. Т. 7. — М., 2004. — 400 с.
- Łukasiewicz J., Tarski A. Untersuchungen über den Aussagenkalkül // Sprawozdania z posiedzec Towarzystwa Naukowego Warszawskiego. Wydział II. R. XXIII. — Warszawa, 1930.
- Формальная логика // Розенталь М., Юдин П. (ред.). Краткий философский словарь. — М.: .
- Ладенко И. С. Становление и развитие идей генетической логики // Вопросы методологии, 1991, № 3.
- ↑
- Постановление ЦК ВКП(б) от 03.12.46 «О преподавании логики и психологии в средней школе».
- «Основы теоретической логики» Гильберта и В. Аккермана (1947), «Опыт исследования значения логики» Ш. Серрюса (), «Введение в логику и методологию дедуктивных наук» А. Тарского (1948) и др.
Умозаключение
Умозаключение – это форма мышления, в которой из двух или нескольких суждений, называемых посылками, вытекает новое суждение, называемое заключением (выводом). Например:
- Все животные нуждаются в корме.
- Лошади – это животные.
- Лошади нуждаются в корме.
В приведенном примере первые два суждения являются посылками, а третье – выводом (умозаключением).
Имейте в виду, что посылки должны быть не только истинными суждениями, но и связанными между собой.
Умозаключения делятся на три вида:дедуктивные, индуктивные и умозаключения по аналогии.
Дедуктивные умозаключения (дедукция) (от лат. deductio — «выведение») – это умозаключения, в которых из общего правила делается вывод для частного случая. Например:
- Все хищники питаются мясом.
- Львы – это хищники.
- Львы питаются мясом.
Основное достоинство дедукции заключается в достоверности ее выводов. Известный персонаж Шерлок Холмс пользовался дедуктивным методом при раскрытии преступлений.
Однажды, объясняя доктору Ватсону суть дедуктивного метода, он привел такой пример. Около убитого полковника была найдена выкуренная сигара, вследствие чего сыщики Скотленд-Ярда решили, что именно он выкурил ее перед смертью. Но Холмс отвергает эту версию на основании того, что полковник носил большие усы, а сигара выкурена до конца.
Иначе говоря, если бы ее курил убитый, то он обязательно бы подпалил свои усы. Следовательно, делает дедуктивное умозаключение Холмс, сигару выкурил другой человек.
Все дедуктивные умозаключения называются силлогизмами (от греч. sillogismos – «подсчитывание, подытоживание, выведение следствия»).
Индуктивные умозаключения (индукция) (от лат. inductio — «наведение») – это умозаключения, в которых из нескольких частных случаев выводится общее правило. Например:
- Петя любит играть.
- Ваня любит играть.
- Настя любит играть.
- Петя, Ваня и Настя – дети.
- Все дети любят играть.
Умозаключения по аналогии (аналогия) (от греч. analogia — «соответствие») – это умозаключения, в которых на основе сходства предметов (объектов) в одних признаках делается вывод об их сходстве и в других признаках. Например:
- Мотоциклист Вася обожает свой мотоцикл, быструю езду, ровную дорогу, и недолюбливает машины.
- Мотоциклист Коля обожает свой мотоцикл, быструю езду и ровную дорогу.
- Вероятно, Коля недолюбливает машины.
Помните, что выводы аналогии и индукции всегда вероятностны.
Итак, вы ознакомились с определением науки логики, а также поняли, что собой представляет логическое мышление.
Теперь вам осталось совсем немного, а именно, узнать 4 основных закона логики. После этого вы сможете развивать логическое мышление и определять логические ошибки своих собеседников.
 МИР ЛОГИКИ
МИР ЛОГИКИ