Применение корреляционного анализа в психологии 3259

Применение корреляционного анализа в психологии 3259

Методы корреляционного анализа

Данный анализ может выполняться с использованием:

• метода квадратов или Пирсона;
• рангового метода или Спирмена.

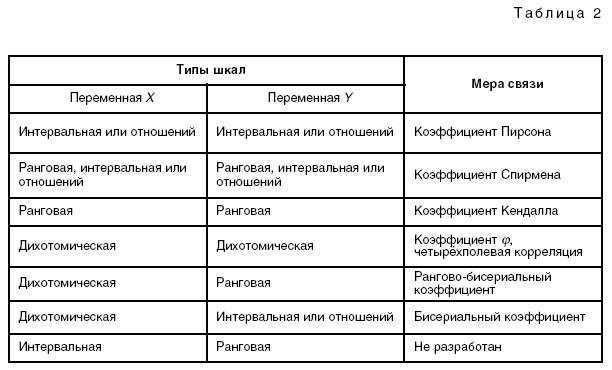
Метод Пирсона применим для расчетов требующих точного определения силы, существующей между переменными. Изучаемые с его помощью признаки должны выражаться только количественно.

Для применения метода Спирмена или ранговой корреляции нет жестких требований в выражении признаков – оно может быть, как количественным, так и атрибутивным. Благодаря этому методу получается информация не о точном установлении силы связи, а имеющая ориентировочный характер.

В рядах переменных могут содержаться открытые варианты. Например, когда стаж работы выражается такими значениями, как до 1 года, более 5 лет и т.д.

Ранги Спирмена

Коэффициент ранговой корреляции Спирмена позволяет статистически установить наличие связи между явлениями. Его расчет предполагает установление для каждого признака порядкового номера – ранга. Ранг может быть возрастающим либо убывающим.

Количество признаков, подвергаемых ранжированию, может быть любым. Это достаточно трудоемкий процесс, ограничивающий их количество. Затруднения начинаются при достижении 20 признаков.

Для расчета коэффициента Спирмена пользуются формулой:

в которой:

n – отображает количество ранжируемых признаков;

d – не что иное как разность между рангами по двум переменным;

а ∑(d2) – сумма квадратов разностей рангов.

Краткая инструкция к проведению корреляционного анализа по критерию Спирмена

Проведение корреляционного анализа с использованием метода Спирмена выполняется по следующему алгоритму:

• парные сопоставимые признаки располагаются в 2 ряда, один из которых обозначается с помощью Х, а другой У;
• значения ряда Х располагаются в порядке возрастания либо убывания;
• последовательность расположения значений ряда У определяется их соответствием значений ряда Х;
• для каждого значения в ряду Х определить ранг — присвоить порядковый номер от минимального значения к максимальному;
• для каждого из значений в ряду У также определить ранг (от минимального к максимальному);
• вычислить разницу (D) между рангами Х и У, прибегнув к формуле D=Х-У;
• полученные значения разницы возводятся в квадрат;
• выполнить суммирование квадратов разниц рангов;
• выполнить расчеты по формуле: