Как работает теория шести рукопожатий

Как работает теория шести рукопожатий

Правда или миф

Верить или нет закону 6 рукопожатий, каждый решает сам. Однако, стоит учитывать, что в научном мире к нему относятся более чем серьезно. Причем ученые, высказывающиеся за данную теорию, работают в самых разных областях, зачастую далеких от социологии, с которой все началось. Одним из наиболее ярких примеров такого отношения ученого мира является игра «Число Эрдеша», названная именем венгерского математика, который написал множество научных работ. Заключается смысл игры в том, что надо найти самую короткую человеческую цепочку, которая ведет от любого наугад выбранного ученого к самому Эрдешу. К примеру, ученому присваивается первый номер, если он в какой-либо отрезок времени работал с основателем игры. Второй номер получает тот ученый, который работал с научным деятелем, в свою очередь трудившимся с самим Эрдешом. Примечательно, что большинство лауреатов Нобелевской премии обладают небольшими числами по этой игре.

К слову, данную теорию может проверить любой желающий, и для этого совсем не надо быть ученым. Все, что для этого надо, это составить собственную «карту знакомств». Желательно, чтобы звеном не ниже четвертого оказалось знакомство с какой-либо знаменитостью. Чем больше его популярность, чем выше вероятность знакомства с огромным количеством людей, в том числе и высокопоставленных, которые, в свою очередь, имеют не меньше знакомых.

Таким образом, возможно, мы все знакомы через 6 рукопожатий. Вследствие детального изучения всех результатов экспериментов, проводимых в разные промежутки времени и различными методами, популярная шутка про знакомство с английской королевой больше не кажется фантастической. Подумайте, с какой знаменитостью, которая до этого времени казалась абсолютно недосягаемой, вы можете оказаться знакомы, согласно данной теории. Вполне вероятно, что результат собственного исследования вас сильно удивит.

Ход эксперимента

Площадками, где проводился эксперимент Милгрэма, стали города Омаха и Уичито, которые находятся, соответственно, в штатах Небраска и Канзас. Адресатом выбрали жителя Бостона. Ученые объяснили свой выбор тем, что, несмотря на небольшую отдаленность городов друг от друга с точки зрения географии, их жителей разделяла целая пропасть по уровню жизни и образования.
Эксперимент заключался в том, жителям Омахи и Уичито, выбранным случайным образом, отправили письма с приглашением принять участие в научном эксперименте. В том случае, если они соглашались, им следовало написать на бланке, вложенном в письмо, свои данные. Затем это письмо нужно было отправить жителю Бостона, имя которого было указано на конверте. Если адресат знал его лично, он должен был переадресовать письмо ему, а если нет, то надо было отправить послание человеку, который с большей вероятностью его знает. Единственным условием было то, что конверт должен пересылаться только лично знакомому человеку или родственнику.

Активная позиция

Вот вы решились принять участие в тематической конференции. Не думайте, что можно просто прийти и поприсутствовать на мероприятии, к нему нужно подготовиться заранее. Ознакомьтесь с тематикой, отметьте полезные выступления, нужных людей, которых вы можете там встретить. Подумайте над темами для разговора с ними во время кофе паузы.

Выпишите в блокнот предполагаемые вопросы, которые вы сможете задать докладчикам. Это очень действенный метод завести профессиональные связи, высказывая свою заинтересованность в том, над чем работает другой человек. Но и задавать вопрос нужно правильно: встаньте, назовите свое имя, фамилию, компанию, в которой вы работаете, затем уже задавайте вопрос. Вступая в дискуссию, избегайте агрессии, демонстрируя уважение к своему собеседнику.

Такие обсуждения полезны вам еще и тем, что на вас обратят внимание авторитеты вашего профессионального сообщества, вас заметят. В конце концов, у вас вряд ли был бы шанс пообщаться с этими людьми в другой ситуации

Экспериментальное подтверждение теории

Предположение, не подтвержденное практикой, так и осталось бы гипотезой и интеллектуальной игрой, поэтому эксперименты проводились регулярно. Первым подтвердить правильность гипотезы о знакомстве всех жителей планеты взялся психолог Стэнли Милгрэм. В 1967 г. американец поставил эксперимент «Тесный мир».

В двух городах США – Омахе и Уичито – отобрали 300 случайных участников, которые должны были связаться письмом с биржевым брокером в Бостоне. Участники не знали адреса, но должны были вычислить его через знакомых. Письмо пересылалось по цепочке, каждый получатель дописывал в нем свое имя. После подведения итогов оказалось, что в среднем цепочка состояла из пяти человек или шести связей.

В дальнейшем эксперименты проводились в других условиях и с различными исходными данными, но результаты всегда оказывались аналогичными и подтверждали правильность гипотезы.

В 1998 году Дункан Уоттс и Стивен Строгатц из Корнеллского университета смогли создать математическую модель и повторили опыт Милгрэма в большом масштабе. В исследовании участвовали десятки тысяч человек из всех уголков мира. Получателями сообщений стали граждане разных стран и континентов, горожане и сельские жители, относящиеся к разным социальным группам. Письма теперь отправляли через интернет, но и в этом случае результат оказался уже известным – цепочки состояли преимущественно из шести звеньев. Кроме этого, с помощью математической модели удалось выяснить любопытные закономерности организации сообществ людей. Оказалось, например, что при глобальных коммуникациях особенно полезны люди, одновременно относящиеся к нескольким группам.

Самым масштабным стало исследование экспертов Microsoft Юре Лесковца и Эрика Хорвитца, проведенное в 2006 году. Исследователи проанализировали более 30 млрд. сообщений через MSN Messenger, отправленных 240 млн. пользователей за 30 дней. На изучение ушло около двух лет. Лесковец и Хорвитц, конечно, не читали тексты сообщений, но видели информацию о людях: пол, возраст, местоположение, периодичность и объем общений, контакты. Итоги трудоемкого изучения информации представляют научный интерес, но нас интересует конкретная тема – между двумя пользователями MSN оказались 6,6 связи. То есть, число, близкое к уже известному нам.

Интернет значительно облегчил коммуникации – в соцсетях есть сервисы, позволяющие проследить цепочку общих друзей, игры по принципу «Тесного мира», сетевые проекты для исследования перспектив глобальных информационных сетей.

Мир тесен

Несмотря на то что данная теория выглядит фантастической на первый взгляд, она существует уже достаточно давно и не раз находила подтверждение.

Сложно сказать, когда появилось выражение «Мир тесен». Скорее всего, оно берет свое начало еще с тех времен, когда люди жили только на своей территории и практически не выезжали за ее пределы. С годами границы расширялись, люди стали сначала ездить друг к другу в гости, а затем и переезжать с насиженных мест в поисках лучшей доли. Однако и в новых местах встречались либо земляки, либо другие люди, с которыми когда-то были знакомы. В крайнем случае в разговорах с новыми людьми практически всегда находились общие знакомые. Именно с тех пор и вошло в наш лексикон данное понятие.

Результат

Главным препятствием к получению точной информации в результате данного эксперимента стало то, что многие из тех, к кому приходили письма на различных этапах его проведения, не соглашались передавать их дальше. Всего ученые отправили 296 конвертов с просьбой об участии, из которых до бостонца дошли только 64. При этом средняя длина каждой цепочки, достигшей цели, составила 5,5-6 человек. Был установлен и еще один интересный факт: некоторые участники выбирали «промежуточное» звено данной цепи, руководствуясь тем, кто из их знакомых живет ближе других к Бостону. Причем именно в таких случаях письма и не достигали до цели.

На основе полученных данных спустя два года была сформулирована теория 6 рукопожатий, которая с развитием Интернета получила новый смысл.

За против идеи 6 рукопожатий

Существуют ли какие-либо ограничения у этой, на первый взгляд, безгрешной теории? Конечно, поскольку несколько столетий назад человечество не было так монолитно и не обладало такими возможностями для перемещения.

На самом деле, правило 6 пожатий не означает автоматически, что каждый из нас может быть знаком с английской королевой или султаном Брунея. Люди склонны формировать сообщества по каким-либо ограниченными признакам, например, по возрасту, по тематическим интересам и так далее. Границы каждого круга знакомств обнаруживаются уже через 2-3 уровня.

Идею, которая подобна гипотезе 6 рукопожатий, раскрывает добрый и трогательный фильм «Елки». В нем действие происходит в различных российских городах, каждый из которых находится в своем собственном часовом поясе. Люди по цепочке передают просьбу ребенка, помочь которому может лично президент, но никто не знаком с ним лично.

Вот с таким интересным правилом, друзья, мы познакомились сегодня, и сопровождающий нас прогресс только подтверждает его. Люди становятся все более коммуникабельными благодаря социальным сетям, онлайн конференциям и другим способам и механизмам общения. Подписывайтесь на обновления блога, и мы с Вами будем и дальше обсуждать полезные и увлекательные события. Пока!

Сегодня Интернет стер все границы, и каждый день миллионы людей из разных стран и континентов знакомятся друг с другом, хотя в реальной жизни вряд ли когда-нибудь могли бы увидеться. Однако немногие знают, что которую сегодня скорее можно было бы назвать теорией шести кликов, была описана в фантастическом рассказе Фридеша Каринти задолго до начала компьютерной эры.

Любое место подойдет

Не стоит доверять судьбе в подобных знакомствах, вы должны использовать любую возможность и сами стремиться к расширению своего круга общения. Недаром нетворкинг – это целое искусство о том, как заводить деловых друзей целенаправленно. Некоторые владеют этим талантом с рождения, другим приходится учиться всю жизнь. Итак, где же знакомиться с людьми?

В первую очередь – на работе. Большее количество связей у самого простого разговорчивого сантехника. За день он посещает много людей и всегда может сделать что-то сверх того, за что уже заплатил хозяин квартиры. Так он уже следует первому правилу нетворкинга, описанному выше. Ему осталось лишь оставить после себя приятное впечатление и свою визитку. Уже через пару лет он запросто сможет открыть свое дело.

Если ваши возможности не настолько безграничны, и большую часть времени вы проводите в офисе, то и здесь есть небанальные варианты. Обязательно посещайте все тематические мероприятия, конференции, форумы, выставки, даже корпоративные вечеринки. Подойдут и курсы повышения квалификации, семинары.

Эксперимент в социальных сетях

С приходом эпохи социальных сетей эксперимент повторили и в них. Наверное, каждый из нас замечал, что принимая приглашение в друзья от незнакомого человека, мы видим одного или двух общих друзей. Удивительно, но эти люди связывали вас долгое время в реальной или в виртуальной жизни и фактически вы были знакомы еще задолго до того момента, как стали общаться в соцсетях. Facebook, являясь на сегодня самой широкой социальной сетью, популярной во всем мире, провел свое исследование совместно с Миланским университетом. И их вердикт: количество звеньев в человеческой цепочке всего 4,4. Конечно, есть погрешность, так как охват регистрации в сети Facebook составляет не 100%.

Граф Мир тесен

Интересно, что, казалось бы, чисто социологическое исследование положило начало развитию целого направления в теории графов. В частности, было введено новое понятие — граф “Мир тесен”, обладающий следующими свойствами: две его произвольные вершины с большой вероятностью не являются смежными, но одна из них достижима из другой посредством небольшого числа переходов через другие вершины. Иначе говоря, граф “Мир тесен” представляет собой сеть, в которой типичное расстояние между двумя любыми вершинами или количество шагов, которые необходимы, чтобы достичь одну из другой, увеличивается пропорционально натуральному логарифму от числа вершин в сети. Причем доказано, что социальные сети, вики-сайты, связность сети Интернет, генные сети и др. довольно хорошо описываются графом “Мир тесен”.

Как проверить гипотезу в соцсетях

Эта теория не так проста для понимания, как может показаться на первый взгляд. Но продемонстрировать ее наглядно помогут социальные сети, например, вконтакте. Во всяком случае, лично мне помог следующий алгоритм:

1. Выбираем в поиске людей любого незнакомого Вам человека (для этого введите имя и фамилию, которые придут в голову)
2. Из выпавшего списка кандидатов можно, не колеблясь, выбрать того, который живет в другом городе, а еще лучше в другой стране
3. Заходим на его страницу, в его список друзей и выбираем первого по списку
4. Теперь посещаем страницу этого первого по списку и смотрим его друзей, и снова выбираем самого первого
5. Повторяем эту операцию до 5-6 раз. Но лично я уже на 3-м человеке обнаружил своих знакомых

Таким образом, правило показывает, что я был знаком с девушкой, которая проживает от меня в тысячах километров и о которой я никогда ничего не слышал, через опосредованную цепочку своих знакомых.

Опыт Милгрема

Оказывается, «мир тесен» – это не только расхожая фраза, но и название любопытного психологического эксперимента, который в 60-х взбудоражил общественность. Тогда американский психолог Стенли Милгрем задумал опыт с целью проверить недавно разработанную гипотезу о связности социальных сетей.

Милгрем подготовил 160 писем и отправил их случайным получателям из Омахи (Небраска). В каждом письме было указано имя биржевого маклера из Шарона (Массачусетс), работавшего в Бостоне, и необычная просьба: надписать на конверте своё имя и отослать его человеку, который мог быть ближе к адресату территориально или профессионально: сестре в Бостон, коллеге из Массачусетса или другу, отец которого трудится на бирже – любому, кто на взгляд получателя мог доставить письмо через минимальное количество пересылок.

Пока конверт переходил от человека к человеку, на нём накапливался список имён, количество которых и анализировал Милгрем. Как выяснилось, в среднем пять-шесть. Сам экспериментатор был очень удивлён результатом, ведь, по оценкам всех, кого он опрашивал, письма должны были миновать сто и больше рук.

Дальше – аналитика. Исследуя пути, по которым были доставлены конверты, Милгрем понял, что более половины из них прошли через руки трёх людей – продавца одежды Джейкобса из магазина рядом с домом маклера, а также двух коллег адресата. То есть несколько десятков независимых цепочек замкнулись всего на трёх людях. Не в этом ли разгадка?

Проверка теории шести рукопожатий 20

• 15.12.15 02:15

•
InspiredByData
•
#273191
•
Хабрахабр

•
Из песочницы

•

•

31000

Python, Data Mining, Вконтакте API

Хочу рассказать о своем эксперименте по проверке «Теории шести рукопожатий». На написание этого материала меня вдохновила статья «Анализ дружеских связей VK с помощью Python» (чтобы избежать повторений, в дальнейшем я буду ссылаться на нее). Так как в целом задача мной была поставлена по-другому, да и использованные методы тоже отличаются, то я решил что это может быть интересно.
Формулировка задачи: визуализировать все связи между двумя пользователями внутри одной социальной сети. При этом связи не должны дублироваться, например если Ваня знает Петю через Олю, то Оля в дальнейших итерациях по поиску общих друзей не участвует. Чтобы попрактиковаться в API, я выбрал “Вконтакте”.
Отталкиваясь от ограничений API и функциональности методов, было решено, что оптимальным количеством «рукопожатий» с позиции времени получения информации будет 3. Так что проверять все-таки будем «Теорию трех рукопожатий», пока что. Таким образом при среднем количестве друзей 200, мы получаем выборку из 8 млн. человек. Например, в масштабах Украины я практически всегда находил связи.?? Структурно задачу можно разбить на следующие этапы: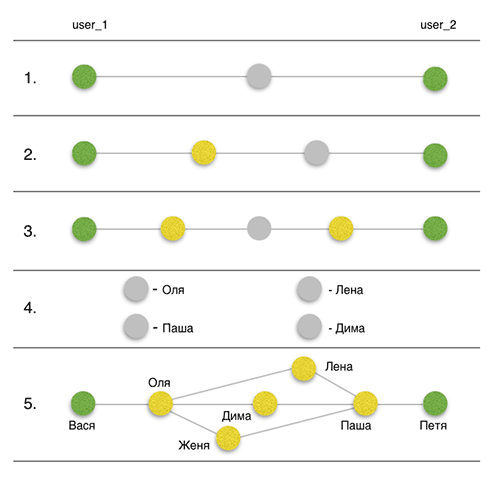

1. Поиск общих друзей между исходным пользователем 1 (user_1) и исходным пользователем 2 (user_2).
2. Поиск общих друзей между user_2 и друзьями user_1.
3. Поиск общих друзей между друзьями user_2 и друзьями user_1.
4. Получение детальной информации о найденных связях.
5. Визуализация.

Requests«Библиотека для упрощения HTTP-запросов»TimeThreading«Учимся писать многопоточные и многопроцессные приложения на Python»исходной статьестранице API «Вконтакте»

• Для обращения к методу API используется POST или GET запрос.
• Список использованных мной методов: users.get, friends.get, friends.getMutual, execute.
• Метод execute позволяет запускать до 25 методов одним запросом.
• В секунду можно осуществить не более 3 запросов (используя один токен).
• Ограничение для параметра target_uids метода friends.getMutual — 300. Об этом более подробно остановлюсь ниже.

executeSTLEONfriends.getMutual

Этап 1. Поиск общих друзей между user_1 и user_2

• method — название метода, к которому мы обращаемся через API.
• parameters — параметры этого метода (можно найти в описании каждого метода).
• token — строка, которая авторизирует Вас на сервере. Повторюсь, что получение токена подробно описано здесь и здесь.

friends.get

friends.getMutual

friends.getMutual

try-except

Этап 3. Поиск общих друзей между друзьями user_2 и друзьями user_1

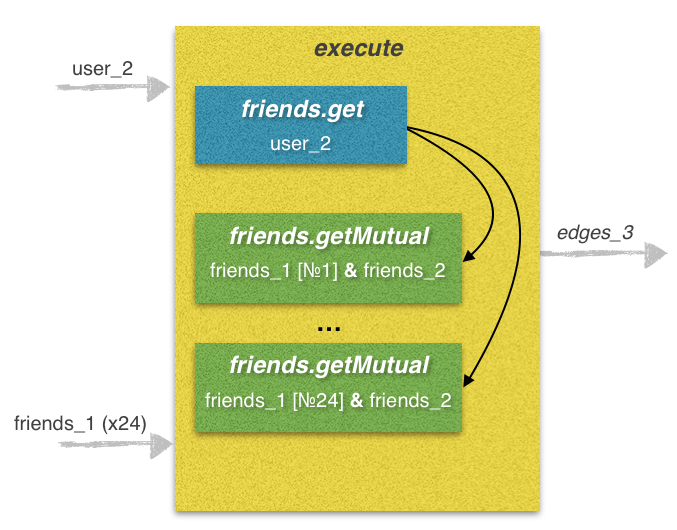
executefriends.getfriends.getMutualexecute«Учимся писать многопоточные и многопроцессные приложения на Python»

Этап 5. Визуализация

networkxD3.js“Radial Reingold–Tilford Tree”СherryPyрепозитории GitHubD3.js“Radial Reingold–Tilford Tree”D3.jsD3 Dependencies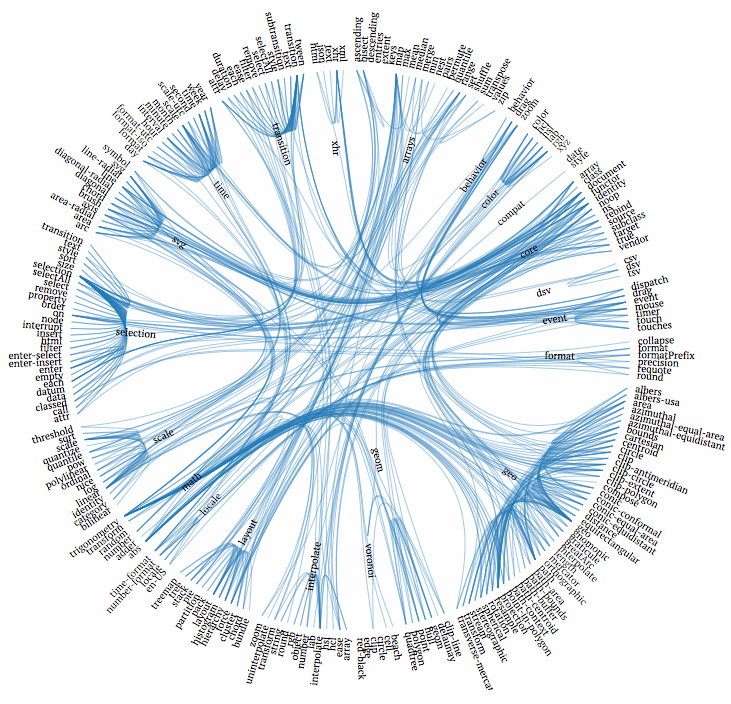

Вы можете помочь и перевести немного средств на развитие сайта

Короткие цепи

Малкольм Глауделл, канадский журналист и автор книг по популярной психологии и социологии, называет таких людей «объединителями» и утверждает, что большинство социальных связей возможны благодаря ним – людям с очень широким кругом знакомств. Грубо говоря, не любой человек «А» связан с любым другим человеком «Б» через шесть приёмов, а есть несколько объединителей с огромным количеством контактов, которые через небольшое число рукопожатий связаны между собой и с «обычными» людьми вроде пресловутых «А» и «Б». Кстати, в наш век Интернета, когда у многих есть привычка сохранять знакомства с шапочно знакомыми людьми через соцсети, эти цепи рукопожатий могут быть ещё короче.

Вернёмся к нашим предположениям в начале статьи. Знакомство с французским президентом – шутка? Не совсем. Другая шутка о знакомстве любого из нас с английской королевой через пять шагов возникла после проведённого Microsoft анализа данных более 240 миллионов пользователей. Количество выявленных в их исследовании «рукопожатий» между любым «А» и любым «Б» – 6,6. Другой эксперимент – Facebook — определил эту цифру в 4,74.

Австралийский фермер? И снова не шутка. В 2012 году в Columbia Magazine была опубликована статья об исследовании колумбийских учёных, которые предложили добровольцам найти человека в любой точке мира по его имени, месту жительства и профессии с помощью электронной почты. В ходе этого эксперимента австралийский резидент всего через четыре сообщения «нашёл» адресата из Сибири.

Ну ладно, с крестьянином из Никарагуа может так просто и не получиться. В конце концов число рукопожатий, будь то четыре, пять или шесть с половиной, – это среднее количество. Тем не менее сама возможность такого (любого!) знакомства в нашем «тесном» мире, согласитесь, захватывает.

Подтверждение правила 6 рукопожатий современными технологиями

Дальше – больше: с развитием технологий ученые смогли высчитать данный алгоритм математическим путем. Одно из масштабных исследований было с размахом проведено в 2006-м году сотрудниками компании Microsoft. Они обработали миллиарды сообщений, отправленных пользователями в течение месяца. Оказалось, что показатель среднего расстояния между 2-мя пользователями составил величину 6,6.

Как только интернет стал общераспространенным явлением, принцип доступности любого пользователя стал еще более очевидным и легко доказуемым, благодаря ВК, FaceBook, LiveJournal и другим ресурсам, объединяющим людей из различных отдаленных уголков земного шара.

Сегодня даже работают сервисы, которые помогают установить цепочку от одного пользователя к другому. Возможности глобальной коммуникации изучаются разнообразными сетевыми проектами и приложениями.