Психологические
В приведенных ниже стихах, взятых из одного английского журнала, выходившего в прошлом веке, рассказывается о хитром хозяине гостиницы, сумевшем разместить в девяти номерах десять гостей так, что каждому из них досталось по отдельной комнате.
Их было десять чудаков,Тех спутников усталых,Что в дверь решили постучатьТаверны «Славный малый».— Пусти, хозяин, ночевать,Не будешь ты в убытке,Нам только ночку переспать,Промокли мы до нитки.Хозяин тем гостям был рад,Да вот беда некстати:Лишь девять комнат у негоИ девять лишь кроватей.— Восьми гостям я предложуПостели честь по чести,А двум придется ночь проспатьВ одной кровати вместе.Лишь он сказал, и сразу крик,От гнева красны лица:Никто из всех десятерыхНе хочет потесниться.Как охладить страстей тех пыл,Умерить те волненья?Но старый плут хозяин былИ разрешил сомненья.
Софизм в споре
Зачастую подобный прием используется при аргументации своей позиции
Еще раз рекомендуется обратить внимание, что простая ошибка и софизм различны только в психологическом плане
Рассмотрим пример. Если кто-либо в споре отступает от заявленного в начале дискуссии тезиса, но не замечает этого – это ошибка. В ситуации, когда человек преднамеренно уходит от исходной посылки, надеясь, что оппонент не увидит или не поймет, – это уже будет софизмом.
Примеры софизмов в дискуссии
Для наглядности рассмотрим, какими бывают софизмы?
- Неопределенности. Это случается, когда доказывающий говорит так, чтобы его невозможно было понять, отвечая на конкретно поставленный вопрос неоднозначно. Из слов человека не получается понять значение и смысл.
- Отступлением от тезиса. Иногда это происходит, если противник начинает разбирать и доказывать не истинность или ложность исходной посылки, а аргументацию своего оппонента. Можно увидеть подобную ситуацию в суде, когда адвокат разбивает все доказательства вины подсудимого, приведенные прокурором, после чего делает вывод, звучащий, как «подсудимый невиновен». Хотя при этом правильным умозаключением было бы: «вина не доказана».
- Подмена пункта разногласия. Такой софизм случается, если противник не опровергает исходную мысль в целом, а выступает против лишь некоторых ее частностей. А когда он доказывает их ложность, делает вывод, что весь тезис также неправдив. Приведем пример. В статье указано, что мэр города Н. выслал из города гражданина Лимонова. После этого выходит опровержение главы поселения: «В городе Н. нет и не было людей с фамилией Лимонов». То есть в личных данных высланного была допущена ошибка. Мэр воспользовался этим и оставил без ответа сообщение в целом, опровергнув лишь его часть. Таким образом, произошла ошибка, в которой существенный момент разногласия подменили неважным и незначительным.
Софизмы зачастую настолько неоднозначны, что подкупают человека своей внешней убедительностью. Однако при ближайшем рассмотрении можно распознать и выявить логические ошибки и ложные элементы.
Итак, софизмом называется рассуждение, которым умышленно обосновывается изначально нелепый, бессмысленный тезис. Теоретический анализ их был проведен Платоном через его «Диалоги». Однако систематическое рассмотрение, основанное на силлогизме и подобных умозаключениях, провел Аристотель. Софизм получил свое название благодаря группе древнегреческих мыслителей, которые прививали молодым людям искусство спора, а именно учили доказывать любой тезис, не заботясь о его истинности
Важно было лишь выйти победителем из дискуссии
Софизмы активно используются и в наше время, а его основной задачей является манипуляция общественным сознанием. Сейчас это активно применяется специалистами по пиару, политиками во время предвыборных кампаний и адвокатами на судебных заседаниях. Таким образом, под софизмом понимается преднамеренный обман, основанный чаще всего на нарушении правил логики.
Софистика
Всем хорошо известна фраза «человек есть мера всех вещей». Именно это предложение и отражает основную суть этой науки.
Софистика представляет собой научное философское направление, которое возникло в пятом веке в Греции. Отцом софистики считается Протагор.
Это учение явилось спасением для множества ораторов и возрастающего числа общественных дебатов и дискуссий. Софистика наделила людей многозначностью и новым логическим направлением.
Эта наука положила в основу относительность истины, которую можно оспорить при новом подходе к получению знаний. Она опирается на построение новых нетипичных связей и другое толкование предметов и явлений.
Софистика не приемлет абсолютных истин и готова каждую поставить под сомнение.
С одной стороны это направление имело практическую цель — подготовить искусных ораторов, которые сумели бы убеждать и организовывать народ в нужном ключе.
Бурное развитие этой школы связано с построением нового демократического общества в Греции и большой необходимости умелых глашатаев и ораторов для побуждения людей к определенным действиям.
Софисты имели практические занятия, практики и на выходе действительно становились яркими представителями своего дела. Это направление тесно переплеталось с риторикой, однако имело более определенное назначение.
Эти люди активно распространяли свое учение, путешествуя по городам. Постепенно сложилось «старшее» поколение софистов, которое уже затрагивало более сложные проблемы государственности и религии.
В частности поднимался вопрос о существовании богов — ставилось под сомнение наличие Олимпа богов и критиковались основные стопы веры.
Софистика внесла большой вклад в развитие образование и обучения: ее представители активно распространяли знания и необходимость их получать. Можно сказать что благодаря им зародилось критическое мышление.
Основные положения этого направления:
- Попытка выйти за границы привычной логики.
- Многозначное понимание всех вещей.
Критическое отношение к истинам, предложенным как нечто неоспоримое.
Развитие многостороннего подхода к решению проблемы.
Искусное использование логических доводов в определенном направлении.
Развитие багажа знаний и интеллектуального опыта.
Активное познание окружающего мира.
Развитие красноречия и ораторского искусства.
Это учение активно подвергалось критике как во времена основателей, так и в недавние годы.
Наличие «кривой» логики ставили под сомнение получившиеся выводы, а стремление подвергнуть критике и новому пересмотру уже доказанные явления и понятия наталкивало противников софистики на мысль о некомпетентности в оспариваемом вопросе.
На самом деле софисты обладали и обладают большим количеством знаний, но доля истины в этой критике имеется: зачастую информация использовалась в определенных целях и обрабатывалась для этого нужным образом.
При этом софисты во многом опирались на психологическое познание аудитории: какие аргументы и в какой форме будут воздействовать на слушателей.
Для женщин большое значение имеет обилие сравнений и чувственных характеристик и эмоциональная окраска, для мужчин множество фактов и цифр, а также логических связей, пусть и в новом свете.
То есть софистика включает в себя многие элементы психологии внушения и поведения. Современная критика опирается на недостаточное фактическое обоснование выводов софистов и характеризует эти принципы как болезненное мудрствование или умствование.
Это означает бездоказательные пространные рассуждения без конкретной доказательной базы. В эпоху доказательной медицины, экономики и складывании общества потребления такие методы могут показаться неэффективными для воздействия на большие массы людей.
На современном этапе это направление бурно развивается. Средства массовой информации активно пользуются приемами софистов. Также растет интерес к развитию ораторского мастерства и нюансов логического толкования этой древней школы.
Этот подход активно используется при ведении диалогов и переговоров, в политике и дипломатическом искусстве. То есть проблема алогичности решается человеческим фактором и особенностями восприятия.
Классификация ошибок
Логические
Так как обычно вывод может быть выражен в силлогистической форме, то и всякий софизм может быть сведён к нарушению правил силлогизма. Наиболее типичными источниками логических софизмов являются следующие нарушения правил силлогизма:
1. Вывод с отрицательной меньшей посылкой в первой фигуре: «Все люди суть разумные существа, жители планет не суть люди, следовательно, они не суть разумные существа»;
2. Вывод с утвердительными посылками во второй фигуре: «Все, находящие эту женщину невинной, должны быть против наказания её; вы — против наказания её, значит, вы находите её невинной»;
3. Вывод с общим заключением в третьей фигуре: «Закон Моисеев запрещал воровство, закон Моисеев потерял свою силу, следовательно, воровство не запрещено»;
4. Особенно распространённая ошибка quaternio terminorum, то есть употребление среднего термина в большой и в меньшей посылке не в одинаковом значении: «Все металлы — простые тела, бронза — металл: бронза — простое тело» (здесь в меньшей посылке слово «металл» употреблено не в точном химическом значении слова, обозначая сплав металлов): отсюда в силлогизме получаются четыре термина.
Терминологические
Грамматические, терминологические и риторические источники софизмов выражаются в неточном или неправильном словоупотреблении и построении фразы (всякое quaternio terminorum предполагает такое словоупотребление); наиболее характерные:
1. ошибка гомонимия (aequivocatio), например: реакция, в смысле химическом, биологическом и историческом; доктор это как врач и как учёная степень.
2. Ошибка сложения — когда разделительному термину придается значение собирательного. Все углы треугольника больше 2 π в том смысле, что сумма меньше 2 π.
3. Ошибка разделения, обратная, когда собирательному термину дается значение разделительного: «все углы треугольника равны 2 π» в смысле «каждый угол равен сумме 2 прямых углов».
4. Ошибка ударения, когда подчёркивание повышением голоса в речи и курсивом в письме определенного слова или нескольких слов во фразе искажает её первоначальный смысл.
5. Ошибка выражения, заключающаяся в неправильном или неясном для уразумения смысла построении фразы, например: сколько будет: дважды два плюс пять? Здесь трудно решить имеется ли в виду 2*2+5=9 или 2*(2+5)=14.
· Более сложные софизмы проистекают из неправильного noстроения целого сложного хода доказательств, где логические ошибки являются замаскированными неточностями внешнего выражения. Сюда относятся:
1. petitio principii: введение заключения, которое требуется доказать, в скрытом виде в доказательство в качестве одной из посылок. Если мы, например, желая доказать безнравственность материализма, будем красноречиво настаивать на его деморализующем влиянии, не заботясь дать отчет, почему именно он — безнравственная теория, то наши рассуждения будут заключать в себе petitio principii.
2. Ignoratio elenchi заключается в том, что мы, возражая на чье-нибудь мнение, направляем нашу критику не на те аргументы, которые ей подлежат, а на мнения, которые мы ошибочно приписываем нашим противникам.
3. A dicto secundum ad dictum simpliciter представляет заключение от сказанного с оговоркой к утверждению, не сопровождаемому этой оговоркой.
4. Non sequitur представляет отсутствие внутренней логической связи в ходе рассуждения: всякое беспорядочное следование мыслей представляет частный случай этой ошибки.
Психологические
Психологические причины софизмов бывают троякого рода: интеллектуальные, аффективные и волевые. Во всяком обмене мыслей предполагается взаимодействие между 2 лицами, читателем и автором или лектором и слушателем, или двумя спорящими. Убедительность софизма предполагает два фактора: α — психические свойства одной и β — другой из обменивающихся мыслями сторон. Правдоподобность софизма зависит от ловкости того, кто защищает его, и уступчивости оппонента, а эти свойства зависят от различных особенностей обеих индивидуальностей.
Забавные софизмы
Эти философские уловки всегда использовались для того, чтобы ввести собеседника в заблуждение, а иногда над ним и потешиться. Следующие примеры логических софизмов показывают, что авторы древности не были лишены чувства юмора. Например:
Чтобы видеть, глаза человеку не нужны. Ведь он видит без правого глаза. И без левого он тоже способен видеть. Стало быть, глаза не являются необходимым условием, чтобы называться зрячим.
Следующий софизм построен в форме диалога, в котором мудрец задает вопросы крестьянину:
— А что, крестьянин, есть ли у тебя собака?
— Да, есть.
— Есть ли у нее кутята?
— Да, недавно появились на свет.
— Иными словами, получается, что эта собака – мать?
— Именно так, моя собака – мать.
— И эта собака твоя, крестьянин, не так ли?
— Моя, я же тебе сказал.
— Вот, ты сам признал, что твоя мать – собака. Значит, ты – пес.
И еще несколько примеров древних софизмов:
- Что человек не терял, то у него есть. Рога он не терял. Значит, у него есть рога.
- Чем больше самоубийц, тем меньше самоубийц.
- Девушка – это человек. Девушка является молодой, а значит, она – молодой человек. Последний, в свою очередь, является парнем. Стало быть, девушка не является человеком, так как здесь наблюдается противоречие. (Данный софизм является доказательством от противного).
Эти 5 примеров софизмов показывают, что с мудрецами лучше не спорить, по крайней мере, до той поры, пока не обретены навыки логического мышления.
Логический парадокс «Миссионер»
Попав к людоедам, миссионер понял, что его скоро съедят, но при этом у него была возможность выбрать – сварят его или зажарят. Миссионер должен был произнести утверждение, и если оно окажется истинным, тогда его приготовят первым способом, а ложь приведет ко второму способу. Сказав фразу, «вы зажарите меня», миссионер тем самым обрекает людоедов на неразрешимую ситуацию, в которой они не могут решить каким способом его приготовить. Зажарить его людоеды не могут – в этом случае он окажется прав и они обязаны сварить миссионера. А если неправ – то зажарить, но и этого сделать не получится, так как тогда слова путешественника будут истинными.
Интеллектуальные и аффективные причины
Развитая интеллектуальная личность имеет возможность следить не только за своей речью, но еще и за каждым аргументом собеседника, обращая при этом свое внимание на аргументы, приводимые собеседником. Такого человека отличает больший объем внимания, умение искать ответ на неизвестные вопросы вместо следования заученным шаблонам, а также большой активный словарный запас, при помощи которого мысли выражаются наиболее точно
Объем знаний тоже имеет немаловажное значение. Умелое применение такого вида нарушений, как софизмы в математике, недоступно малограмотному и не развивающемуся человеку
К таковым относится боязнь последствий, из-за чего человек не способен уверенно высказать свою точку зрения и привести достойные аргументы. Говоря об эмоциональных слабостях человека, нельзя забывать о надежде найти в любой получаемой информации подтверждение своих взглядов на жизнь. Для гуманитария могут стать проблемой математические софизмы.
Логический парадокс «Крокодил»
У жительницы Египта крокодил выхватил ребенка, но, сжалившись над женщиной, после ее мольбы он выдвинул условия: если она угадает, вернет ли он ей ребенка или нет, то он, соответственно, отдаст или не отдаст его. После этих слов мать задумалась и сказала, что ребенка он ей не отдаст.
На это крокодил ответил: ребенка ты не получишь, ведь в случае, когда сказанное тобой правда, я не могу отдать тебе ребенка, так как если отдам, твои слова уже не будут истинными. А если это неправда – я не могу вернуть ребенка по уговору.
После чего мать оспорила его слова, говоря, что он в любом случае должен отдать ей ребенка. Слова обосновывались следующими доводами: если ответ был правдой, то по договору крокодил должен был вернуть отнятое, а в противном случае он также обязан отдать ребенка, ведь отказ будет означать, что слова матери справедливы, а это опять же обязывает вернуть малыша.
Примеры
Примеры с ответами:
- Один из самых известных примеров является «рога». Эта фраза звучит так: то, чего у вас нет в наличии нельзя потерять. Значит если вы что-то не теряли, то логично рассудить что оно у вас есть. Вы не теряли рога? Значит они у вас есть. Эта логика не имеет фактического доказательства, ведь рогов у Вас нет, но рассуждая и строя логическую цепочку можно прийти к совсем обратному выводу.
- Также построен пример «динозавр». На вопрос встретите ли вы за углом динозавра можно ответить только двумя вариантами — да или нет. Таким образом это половина от вероятности встрерить его наверняка. ,то есть вы имеете пятидесятипроцентную вероятность встретиться с динозавром за углом. Хотя все мы знаем что они давным давно вымерли.
Но такая логика может убедить нас в другом, с чем трудно поспорить.
- «Лекарство». Прием лекарственных средств означает пользу для пациента, потому как лечит его проблему и помогает чувствовать себя лучше. Отсюда следует, что чем больше лекарств вы принимаете, тем вам лучше. Но все врачи сходятся во мнении что в реальности все наоборот: побочные действия препаратов и их взаимодействие могут больше навредить.
«Глаза». Вам не нужны глаза чтобы видеть. Закройте один глаз — вы может видеть другим, а теперь закройте его — вы видите первым глазом. То есть правый и левый глаз не нужны вам для зрения — поздравляем, вы можете видеть без глаз.
«Доброе воровство». Воровство — это добро. Вор не крадет что-то плохое, он непременно положит глаз на что-либо ценное или важное, то есть по своей сути он желает добра, а не зла (никакой вор не украдет невыплаченный кредит или грязную половую тряпку). Однако воровство — это наказуемое деяние.
«Пусто и полно». Известная фраза «стакан наполовину пуст или наполовину полон» у софистов имеет особое толкование. Полупустая или наполовину полная емкость означает что в ней присутствует половина-чего-либо или пустоты.
Значит оба этих понятия равнозначны, и ваш стакан и пуст и полон одновременно.
Математические уловки: 4=5. Известно что 4 можно поделить на 4, а 5 можно поделить на 5. То есть мы получим единицу в обоих случаях, а один равно одному. Значит и четыре равно пяти. Отсюда можно перейти к другому примеру — дважды два равно пять. 2 умножить на 2 равно четыре, а четыре как мы уже доказали равно пяти. Значит дважды два равно пяти.
Литературный пример: в произведении Гоголя «Мертвые Душ» помещик Ноздрев назван исторической личностью, поскольку он часто попадал в различные истории. При этом понятно что в реальной истории страны этот персонаж не имел никакой роли, но двойная трактовка определения позволяет иначе выстроить предложение и его смысл.
«Сократ — это не Сократ». Этот пример один из самых известных. Мы знаем что Сократ — это человек, но любой человек это не обязательно Сократ, а даже кто-то другой, а не Сократ. Значит Сократ не является Сократом.
Разные числа. Три и четыре представляют собой разные числа — это всем понятно. А в сумме они дают семь, значит семь представляет собой разные числа.
Софизм является одним из самых древних, но самых применяемых в современности направлений философии. Из этой области оно перешло в социальную жизнь людей и прочно заняло место в политическом и ораторском искусстве.
Софисты используют иную логику рассуждений и получают новые, отличные от прежних результаты.
Такой прием требует большого мастерства и обучения вопреки распространенному мнению об отсутствии специальных знаний и интеллекта.
Софизмы — понятие и примеры:
Наша интересная группа Вконтакте:
Однако, когда мы имеем полный квадрат , то /х-2а/=/х/, а так x=a, то 2а-x=x.
5. Все числа равны между собой.
Возьмем любые два числах, у. Рассмотрим тождествох2 – 2ху +у2 =у2 – 2ху +х2. Имеем(х — у)2 = (у – х)2. Отсюдах-у = у-хили2х= 2у, а, значит,х = у.
Ошибка заключается в том, что из равенства(х — у)2 = (у – х)2следует, что, а это равенство справедливо для любых чиселу, х.
6. 1=0.
Возьмем уравнениеx-a=0. Разделив обе его части нах-а,получимх-а/х-а=0/х-а. Откуда сразу же получаем требуемое равенство1=0.
Однако в данном софизме используется распространенная ошибка, а именно деление на.
7. Всякое число равно своему удвоенному значению.
Запишем очевидное для любого числа а тождество2а-2а= 2а-2а. Вынесем а в левой части за скобку, а правую часть разложим на множители по формуле разности квадратов, получив:а(а-а)=(а+а)(а-а) (1)
Разделив обе части наа-а,получим а=а+а, а=2а.
В данном софизме вновь используется деление на нуль неравенства (1)(а-а=0 ).
8. Если одно число больше другого, то эти числа равны.
Возьмем два произвольных числаХиУ, такие, чтоХ > У, и другие три произвольных числаа, bис, сумма которых равнаd , т.е. а+ b + c = d. Умножив обе части этого равенства наХ, а затем наУ, получим: Хa+Хb+Хc=Хd, Уa+Уb+Уc=Уd. Сложив почленно эти равенства получимХa + Хb + Хc + Уd = Уa + Уc + Уb + Хd. Перенося здесьУdвправо, аХdвлево, имеем Хa+Хb+ХcХd=Уa+Уb+УcУd.
Вынося слева числоХ, а справа числоУза скобки, придем к соотношению m(a+b+cd)=n(a+b+cd). (1)
Разделив обе части последнего равенства на( a + b + c d ), находим, что, У=Х.
Ошибка, как и в предыдущих примерах заключается в делении на, то есть на( a + b + c d ).
9. Любое число а равно меньшему числу b.
Начнем с равенства а = b + c.
Умножив обе его части на a — b, получим а² — аb = аb + аc — b² — be.Перенесем ас в левую часть: а² — аb — аc = аb — b² — be и разложим на множители: а(а — b — c) = b(а — b — c).Разделив обе части равенства на а — b — c, найдем а = b, что и требовалось доказать.
Арифметические софизмы –это числовые выражения, имеющие неточность или ошибку, не заметную с первого взгляда. Рассмотрим некоторые из арифметических софизмов.
1. Дважды два – пять.
Пусть исходное соотношение — очевидное равенство: 4:4= 5:5 (1) .
Вынесем за скобки общий множитель каждой чести (1) равенства, и мы получим: 4*(1:1)=5*(1:1).(2)
Разложим число 4 на произведение2 *2.
(2*2)* (1:1)=5*(1:1). (3)
Наконец, зная, что1:1=1, мы из соотношения (2) устанавливаем:2*2=5.
Ошибка заключается в том, что нельзя было выносить множитель за скобки в уравнение (2).
2. Один рубль не равен ста копейкам.
Известно, что любые два неравенства можно перемножать почленно, не нарушая при этом равенства, т.е. Еслиa=b, c=d, то ac=bd.
Применим это положение к двум очевидным равенствам 1 р.=100 коп, (1)
10р.=10*100коп. (2)
Перемножая эти равенства почленно, получим10 р.=100000коп.
Наконец, разделив последнее равенство на10получим, что1 р.=10 000коп., таким образом, один рубль не равен ста копейкам.
Ошибка, допущенная в этом софизме, состоит в нарушении правил действия с именованными величинами: все действия, совершаемые над величинами, необходимо совершать также и над их размерностями.
3. Число, равное другому числу, одновременно и больше, и меньше его.
Возьмем два положительных равных числаaиbи напишем для них следующие неравенства:
a > — b и b > — b.
Перемножив оба этих неравенства почленно, получим неравенство a·b>b·b.
Разделим его наb(это законно, т.к.b>0), получимa > b.
Записав же два других столь же бесспорных неравенства:
b > — a и a > — a.
Перемножив оба этих неравенства почленно, получим неравенство b·a > a·a.
Разделив наa>0,придемк b > a.
Итак, число a, равное числу b, одновременно и больше, и меньше его.
Ошибка заключается в неправильном почленном перемножении, вследствие которого место выраженийa>-b;b>-aполучились выраженияa>b; a .
4. 1=2.
Никто не станет возражать, что 3-1=6-4. Умножим обе части равенства на (-1): 1-3=4-6, прибавим к обеим частям равенства одно и тоже число, (9/4):1-3+9/4=4-6 +9/4.
Замечаем, что обе части равенства представляют собой квадраты разностей: (1-3/2)2=(2-3/2)2.
Извлечем из обеих частей квадратный корень: 1-3/2=2-3/2, и теперь к каждой части прибавим 3/2, имеем 1=2.
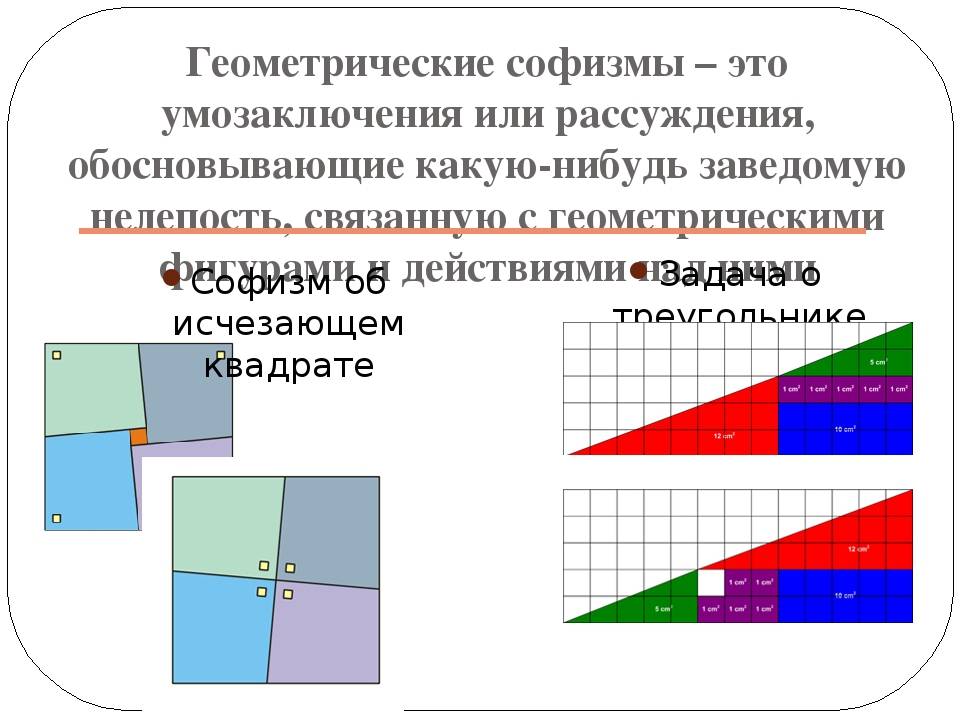
Не менее интересными являются геометрические софизмы, которые основаны на ошибках связанных с геометрическими фигурами и действиями над ними. В качестве примера, рассмотрим следующие софизмы.
1. Спичка вдвое длиннее телеграфного столба.
Софизм «приговор»
Примеры софизмов в философии дополняются «приговором», в котором говорится о том, что некого человека приговорили к смерти, но сообщили об одном правиле: казнь произойдет не сразу, а в течение недели, причем день казни не будет сообщен заранее. Услышав это, приговоренный начал рассуждать, стараясь понять, в какой же день произойдет страшное для него событие. Согласно его соображениям, если казнь не произойдет до самого воскресенья, то уже в субботу он будет знать, что его казнят завтра – то есть правило, о котором ему сказали, уже нарушено. Исключив воскресенье, приговоренный точно так же подумал и о субботе, ведь если он знает, что в воскресенье его не казнят, то при условии, что до пятницы казни не произойдет, суббота тоже исключается. Обдумав все это, он пришел к выводу, что его не могут казнить, так как правило будет нарушено. Но в среду был удивлен, когда появился палач и сделал свое ужасное дело.
Как видно из приведённых выше софизмов, найти ошибки в них не очень сложно, зная основные математические законы и их доказательства. Однако можно выделить несколько основных способов нахождения ошибки в софизме:
-
Внимательно прочитать условие предложенной вам задачи. Начинать поиск ошибки лучше с условия предложенного софизма. В некоторых софизмах абсурдный результат, получается, из-за противоречивых или неполных данных в условии, неправильного чертежа, ложного первоначального предположения, а далее все рассуждения проводятся верно. Это и вызывает затруднения при поиске ошибки. Все привыкли, что задания, предполагаемые в различной литературе, не содержат ошибок в условии и, поэтому, если получается неверный результат, то ошибку они ищут непременно по ходу решения.
-
Установите области знаний (темы), которые отражены в софизме, предложенных преобразованиях. Софизм может делиться на несколько тем, которые потребуют детального анализа каждой из них.
-
Выясните, соблюдены ли все условия применимости теорем, правил, формул, соблюдена ли логичность. Некоторые софизмы построены на неверном использовании определений, законов, на «забывании» условий применимости. Очень часто в формулировках, правилах запоминаются основные, главные фразы и предложения, всё остальное упускается. И тогда второй признак равенства треугольников превращается в признак «по стороне и двум углам».
-
Проверяйте результаты преобразования обратным действием.
-
Часто следует разбить работу на небольшие блоки и проконтролировать правильность каждого такого блока.
Можно бесконечно говорить о софизмах в целом и о математических софизмах в частном. Из года в год появляются новые софизмы, некоторые из них могут остаться в истории, о многих быстро забудут. Ведь софизмы — это смесь математики и логики, поэтому они помогают не только развивать логику, но и лучше понимать математику в целом. В современном мире есть много людей, так или иначе употребляющих софизмы в обычной жизни, даже не зная, что это такое. Есть же и такие люди, которые целенаправленно изучают софизмы, например политики или СМИ, чтобы вводить людей в заблуждение, или просто развить свои навыки логики и правильности рассуждений.
Поначалу может показаться, что существует мало софизмов, или, что они не используются в жизни, то есть бесполезны. Но это не так. Существует огромное множество разных видов софизмов. И математические софизмы – всего лишь небольшая их часть. За свою жизнь человек слышит десятки софизмов, не умея отличить их от правдивых утверждений, и даже не зная, что вообще означает слово софизм.
Понять софизм, то есть решить его, получается не сразу. Поначалу, чтобы решить некоторые софизмы, приходится по многу раз их внимательно перечитывать, вдумываться и всматриваться. В ходе написания данной работы и доказательства софизмов, приведённых в ней, ошибки стали находиться быстрее. Хорошо развитое логическое мышление может помочь не только в решении задач, но и в обычной жизни.
О математических софизмах можно говорить бесконечно много, как и о математике в целом. Изо дня в день рождаются новые парадоксы, некоторые из них останутся в истории, а некоторые просуществуют один день
Вообще, решение софизмов – интересное и познавательное занятие. Им можно заниматься как целенаправленно, так и в свободное время для собственного удовольствия. Изучение математических софизмов раскрывает еще одну страничку в математике, позволяет прикоснуться к тому, с чем сталкивались далекие предки, к теме, которая имеет исторические корни.
Литература
-
Интернет источник https://www.rchgi.spb.ru/Pr/vest_6.htm.
-
Неркарарян К. В., Софизмы и парадоксы, 1 издание, 2001.
 МИР ЛОГИКИ
МИР ЛОГИКИ