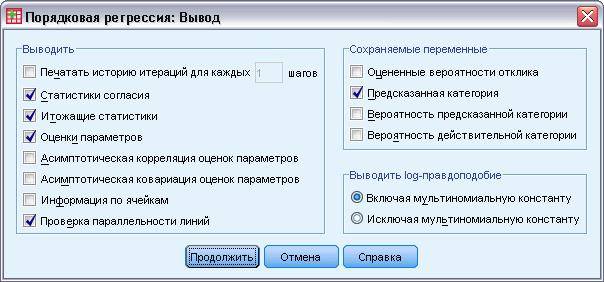
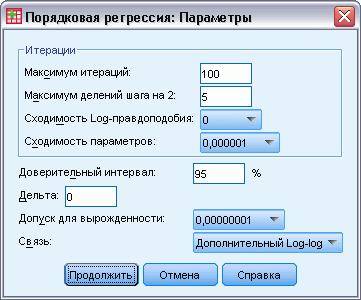
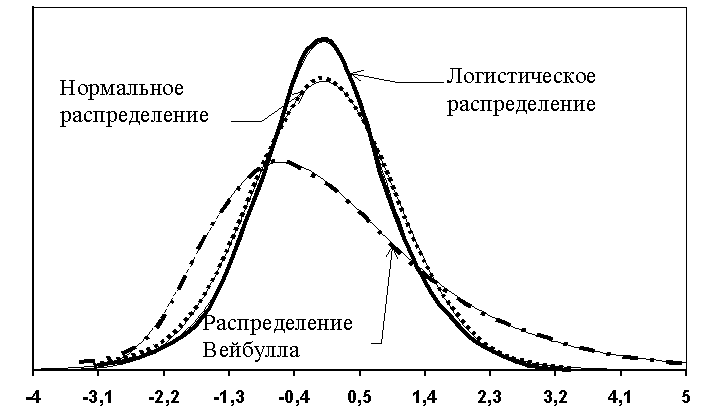
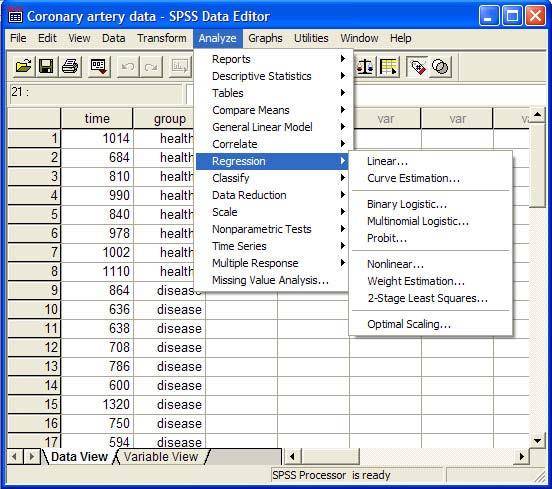
Порядковая регрессия

Порядковая регрессия

Применение линии регрессии для прогноза

Можно применять регрессионную линию для прогнозирования значения по значению в пределе наблюдаемого диапазона (никогда не экстраполируйте вне этих пределов).

Мы предсказываем среднюю величину для наблюдаемых, которые имеют определенное значение путем подстановки этого значения в уравнение линии регрессии.

Итак, если прогнозируем как Используем эту предсказанную величину и ее стандартную ошибку, чтобы оценить доверительный интервал для истинной средней величины в популяции.

Повторение этой процедуры для различных величин позволяет построить доверительные границы для этой линии. Это полоса или область, которая содержит истинную линию, например, с 95% доверительной вероятностью.

Подобным образом можно рассчитать более широкую область, внутри которой, как мы ожидаем, лежит наибольшее число (обычно 95%) наблюдений.

Предположения линейной регрессии

Итак, для каждой наблюдаемой величины остаток равен разнице и соответствующего предсказанного Каждый остаток может быть положительным или отрицательным.

Можно использовать остатки для проверки следующих предположений, лежащих в основе линейной регрессии:

Между и существует линейное соотношение: для любых пар данные должны аппроксимировать прямую линию. Если нанести на двумерный график остатки, то мы должны наблюдать случайное рассеяние точек, а не какую-либо систематическую картину.

Остатки нормально распределены с нулевым средним значением;

Остатки имеют одну и ту же вариабельность (постоянную дисперсию) для всех предсказанных величин  Если нанести остатки против предсказанных величин от мы должны наблюдать случайное рассеяние точек. Если график рассеяния остатков увеличивается или уменьшается с увеличением то это допущение не выполняется;

Если допущения линейности, нормальности и/или постоянной дисперсии сомнительны, мы можем преобразовать или и рассчитать новую линию регрессии, для которой эти допущения удовлетворяются (например, использовать логарифмическое преобразование или др.).

О терминах

Термин «регрессия» был введён Фрэнсисом Гальтоном в конце 19-го века.
Гальтон обнаружил, что дети родителей с высоким или низким ростом обычно не наследуют выдающийся рост и назвал этот
феномен «регрессия к посредственности».
Сначала этот термин использовался исключительно в биологическом смысле.
После работ Карла Пирсона этот термин стали использовать и в статистике.

Аппроксимация функций: непрерывная функция  приближает непрерывную или дискретную функцию 

В статистической литературе различают регрессию с участием одной свободной переменной и с несколькими свободными переменными 
одномерную и многомерную регрессию.
Предполагается, что мы используем несколько свободных переменных,
то есть, свободная переменная  вектор .
В частных случаях, когда свободная переменная является скаляром,
она будет обозначаться .
Различают линейную и нелинейную регрессию.
Если регрессионную модель не является линейной комбинацией функций
от параметров, то говорят о нелинейной регрессии.
При этом модель может быть произвольной суперпозицией функций из некоторого набора.
Нелинейными моделями являются, экспоненциальные,
тригонометрические и другие (например, радиальные базисные функции или персептрон Розенблатта),
полагающие зависимость между параметрами и зависимой переменной нелинейной.

Различают параметрическую и непараметрическую регрессию.
Строгую границу между этими двумя типами регрессий провести сложно.
Сейчас не существует общепринятого критерия отличия одного типа моделей от другого.
Например, считается, что линейные модели являются параметрическими, а модели, включающие усреднение зависимой переменной по пространству свободной переменной непараметрическими.
Пример параметрической регресионной модели: линейный предиктор, многослойный персептрон.
Примеры смешанной регрессионной модели: функции радиального базиса.
Непараметрическая модель  скользящее усреднение в окне некоторой ширины.
В целом, непараметрическая регрессия отличается от параметрической тем,
что зависимая переменная зависит не от одного значения свободной переменной,
а от некоторой заданной окрестности этого значения.

Интерполяция: функция  задана значениями узловых точек

Есть различие между терминами: «приближение функций», «аппроксимация», «интерполяция», и «регрессия».
Оно заключается в следующем.

Приближение функций. Дана функция  дискретного или непрерывного аргумента.
Требуется найти функцию  из некоторого параметрическую семейства, например, среди алгебраических
полиномов заданной степени. Параметры функции   должны
доставлять минимум некоторому функционалу, например,

Термин аппроксимация  синоним термина «приближение функций».
Чаще используется тогда, когда речь идет о заданной функции, как о функции дискретного аргумента.
Здесь также требуется отыскать такую функцию , которая проходит наиболее близко ко всем точкам заданной функции.
При этом вводится понятие невязки  расстояния между точками непрерывной функции  и соответствующими точками функции  дискретного аргумента.

Интерполяция функций  частный случай задачи приближения,
когда требуется, чтобы в определенных точках, называемых
узлами интерполяции совпадали значения функции  и
приближающей ее функции . В более общем случае накладываются
ограничения на значения некоторых производных  производных.
То есть, дана функция  дискретного аргумента.
Требуется отыскать такую функцию , которая проходит через все точки .
При этом метрика обычно не используется, однако часто вводится понятие «гладкости» искомой функции.

Регрессия и классификация тесно связаны друг с другом.
Термин алгоритм в классификации мог бы стать синонимом термина модель в регрессии,
если бы алгоритм не оперировал с дискретным множеством ответов-классов, а модель  с непрерывно-определенной свободной переменной.

Регрессия по методу «лассо»

В регрессии лассо, как и в гребневой, мы добавляем условие смещения в функцию оптимизации для того, чтобы уменьшить коллинеарность и, следовательно, дисперсию модели. Но вместо квадратичного смещения, мы используем смещение абсолютного значения:

min || Xw — y ||² + z|| w ||

Существует несколько различий между гребневой регрессией и лассо, которые восстанавливают различия в свойствах регуляризаций L2 и L1:

• Встроенный отбор признаков — считается полезным свойством, которое есть в норме L1, но отсутствует в норме L2. Отбор признаков является результатом нормы L1, которая производит разреженные коэффициенты. Например, предположим, что модель имеет 100 коэффициентов, но лишь 10 из них имеют коэффициенты отличные от нуля. Соответственно, «остальные 90 предикторов являются бесполезными в прогнозировании искомого значения». Норма L2 производит неразряженные коэффициенты и не может производить отбор признаков. Таким образом, можно сказать, что регрессия лассо производит «выбор параметров», так как не выбранные переменные будут иметь общий вес, равный 0.
• Разряженность означает, что незначительное количество входных данных в матрице (или векторе) имеют значение, отличное от нуля. Норма L1 производит большое количество коэффициентов с нулевым значением или очень малые значения с некоторыми большими коэффициентами. Это связано с предыдущим пунктом, в котором указано, что лассо исполняет выбор свойств.
• Вычислительная эффективность: норма L1 не имеет аналитического решения в отличие от нормы L2. Это позволяет эффективно вычислять решения нормы L2. Однако, решения нормы L1 не обладают свойствами разряженности, что позволяет использовать их с разряженными алгоритмами для более эффективных вычислений.

Гипотеза линейной регрессии

При построении линейной регрессии проверяется нулевая гипотеза о том, что генеральный угловой коэффициент линии регрессии β равен нулю.

Если угловой коэффициент линии равен нулю, между и нет линейного соотношения: изменение не влияет на

Для тестирования нулевой гипотезы о том, что истинный угловой коэффициент равен нулю можно воспользоваться следующим алгоритмом:

Вычислить статистику критерия, равную отношению , которая подчиняется распределению с степенями свободы, где стандартная ошибка коэффициента

,

— оценка дисперсии остатков.

Можно рассчитать 95% доверительный интервал для генерального углового коэффициента :

где процентная точка распределения со степенями свободы что дает вероятность двустороннего критерия

Это тот интервал, который содержит генеральный угловой коэффициент с вероятностью 95%.

Для больших выборок, скажем, мы можем аппроксимировать значением 1,96 (то есть статистика критерия будет стремиться к нормальному распределению)

Линейная регрессия

Основная статья: Многомерная линейная регрессия

Линейная регрессия предполагает, что функция  зависит от параметров  линейно.
При этом линейная зависимость от свободной переменной  необязательна,

В случае, когда функция  линейная регрессия имеет вид

здесь   компоненты вектора .

Значения параметров в случае линейной регрессии находят с помощью метода наименьших квадратов.
Использование этого метода обосновано предположением о гауссовском распределении случайной переменной.

Разности между фактическими значениями зависимой переменной и восстановленными называются регрессионными остатками (residuals). В литературе используются также синонимы: невязки и ошибки.
Одной из важных оценок критерия качества полученной зависимости является сумма квадратов остатков:

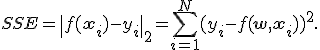
Здесь   Sum of Squared Errors.

Дисперсия остатков вычисляется по формуле

Здесь   Mean Square Error, среднеквадратичная ошибка.

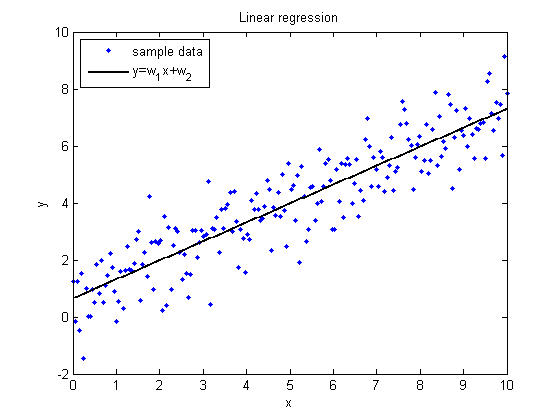
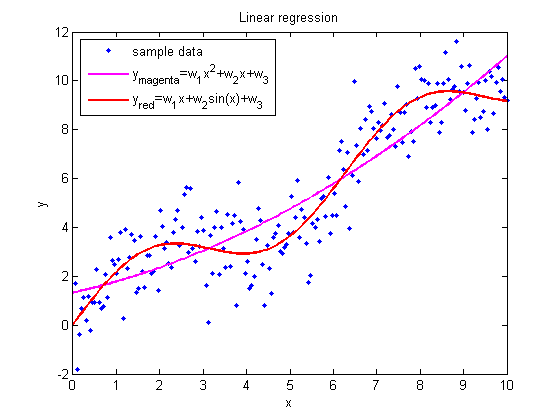
На графиках представлены выборки, обозначенные синими точками, и регрессионные зависимости, обозначенные сплошными линиями.
По оси абсцисс отложена свободная переменная, а по оси ординат  зависимая.
Все три зависимости линейны относительно параметров.

Простые регрессионные планы

Простые регрессионные планы содержат один непрерывный предиктор. Если существует 3 наблюдения со значениями предиктора P, например, 7, 4 и 9, а план включает эффект первого порядка P, то матрица плана X будет иметь вид

а регрессионное уравнение с использованием P для X1 выглядит как

Y = b + b1P

Если простой регрессионный план содержит эффект высшего порядка для P, например квадратичный эффект, то значения в столбце X1 в матрице плана будут возведены во вторую степень:

а уравнение примет вид

Y = b + b1P2

Сигма-ограниченные и сверхпараметризованные методы кодирования не применяются по отношению к простым регрессионным планам и другим планам, содержащим только непрерывные предикторы (поскольку, просто не существует категориальных предикторов). Независимо от выбранного метода кодирования, значения непрерывных переменных увеличиваются в соответствующей степени и используются как значения для переменных X. При этом перекодировка не выполняется. Кроме того, при описании регрессионных планов можно опустить рассмотрение матрицы плана X, а работать только с регрессионным уравнением.

Пример: простой регрессионный анализ

Этот пример использует данные, представленные в таблице:

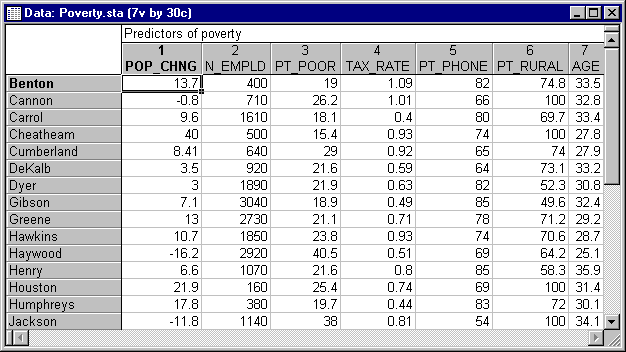
Рис. 3. Таблица исходных данных.

Данные составлены на основе сравнения переписей 1960 и 1970 в произвольно выбранных 30 округах. Названия округов представлены в виде имен наблюдений. Информация относительно каждой переменной представлена ниже:

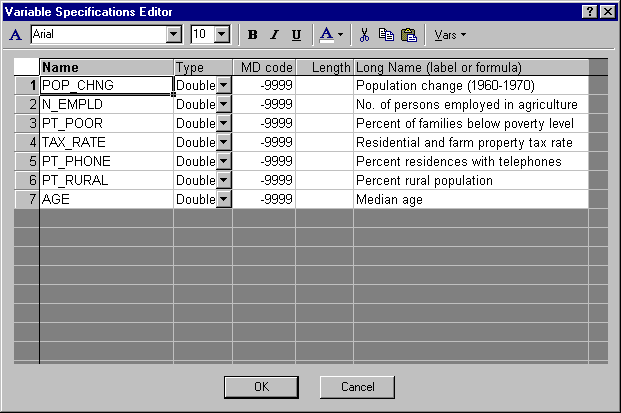
Рис. 4. Таблица спецификаций переменных.

Задача исследования

Для этого примера будут анализироваться корреляция уровня бедности и степень, которая предсказывает процент семей, которые находятся за чертой бедности. Следовательно мы будем трактовать переменную 3 (Pt_Poor) как зависимую переменную.

Можно выдвинуть гипотезу: изменение численности населения и процент семей, которые находятся за чертой бедности, связаны между собой. Кажется разумным ожидать, что бедность ведет к оттоку населения, следовательно, здесь будет отрицательная корреляция между процентом людей за чертой бедности и изменением численности населения. Следовательно мы будем трактовать переменную 1 (Pop_Chng) как переменную-предиктор.

Коэффициенты регрессии

Рис. 5. Коэффициенты регрессии Pt_Poor на Pop_Chng.

На пересечении строки Pop_Chng и столбца Парам. не стандартизованный коэффициент для регрессии Pt_Poor на Pop_Chng равен -0.40374. Это означает, что для каждого уменьшения численности населения на единицу, имеется увеличение уровня бедности на .40374. Верхний и нижний (по умолчанию) 95% доверительные пределы для этого не стандартизованного коэффициента не включают ноль, так что коэффициент регрессии значим на уровне p<.05>

Обратите внимание на не стандартизованный коэффициент, который также является коэффициентом корреляции Пирсона для простых регрессионных планов, равен -.65, который означает, что для каждого уменьшения стандартного отклонения численности населения происходит увеличение стандартного отклонения уровня бедности на .65

Распределение переменных

Коэффициенты корреляции могут стать существенно завышены или занижены, если в данных присутствуют большие выбросы. Изучим распределение зависимой переменной Pt_Poor по округам. Для этого построим гистограмму переменной Pt_Poor.

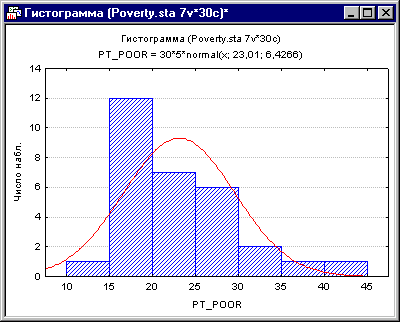
Рис. 6. Гистограмма переменной Pt_Poor.

Как вы можете заметить, распределение этой переменной заметно отличается от нормального распределения. Тем не менее, хотя даже два округа (два правых столбца) имеют высокий процент семей, которые находятся за чертой бедности, чем ожидалось в случае нормального распределения, кажется, что они находятся «внутри диапазона.»

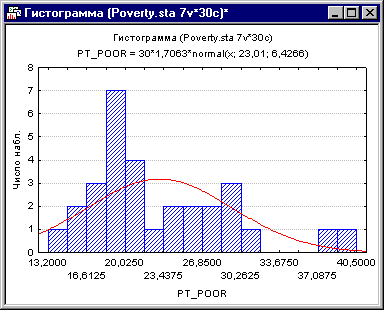
Рис. 7. Гистограмма переменной Pt_Poor.

Это суждение в некоторой степени субъективно. Эмпирическое правило гласит, что выбросы необходимо учитывать, если наблюдение (или наблюдения) не попадают в интервал (среднее ± 3 умноженное на стандартное отклонение). В этом случае стоит повторить анализ с выбросами и без, чтобы убедиться, что они не оказывают серьезного эффекта на корреляцию между членами совокупности.

Диаграмма рассеяния

Если одна из гипотез априори о взаимосвязи между заданными переменными, то ее полезно проверить на графике соответствующей диаграммы рассеяния.

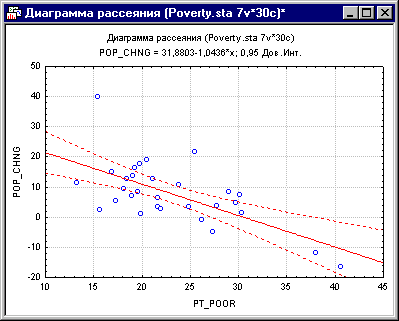
Рис. 8. Диаграмма рассеяния.

Диаграмма рассеяния показывает явную отрицательную корреляцию (-.65) между двумя переменными. На ней также показан 95% доверительный интервал для линии регрессии, т.е., с 95% вероятностью линия регрессии проходит между двумя пунктирными кривыми.

Критерии значимости

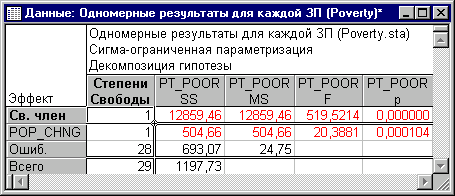
Рис. 9. Таблица, содержащая критерии значимости.

Критерий для коэффициента регрессии Pop_Chng подтверждает, что Pop_Chng сильно связано с Pt_Poor, p<.001>.

Итог

На этом примере было показано, как проанализировать простой регрессионный план. Была также представлена интерпретация не стандартизованных и стандартизованных коэффициентов регрессии

Обсуждена важность изучения распределения откликов зависимой переменной, продемонстрирована техника определения направления и силы взаимосвязи между предиктором и зависимой переменной

Связанные определения:Линейная регрессияМатрица планаОбщая линейная модельРегрессия

Оценка качества линейной регрессии: коэффициент детерминации R2

Из-за линейного соотношения  и мы ожидаем, что  изменяется, по мере того как изменяется , и называем это вариацией, которая обусловлена или объясняется регрессией. Остаточная вариация должна быть как можно меньше.

Если это так, то большая часть вариации  будет объясняться регрессией, а точки будут лежать близко к линии регрессии, т.е. линия хорошо соответствует данным.

Долю общей дисперсии , которая объясняется регрессией называют коэффициентом детерминации, обычно выражают через процентное соотношение и обозначают R2 (в парной линейной регрессии это величина r2, квадрат коэффициента корреляции), позволяет субъективно оценить качество уравнения регрессии.

Разность представляет собой процент дисперсии который нельзя объяснить регрессией.

Нет формального теста для оценки мы вынуждены положиться на субъективное суждение, чтобы определить качество подгонки линии регрессии.

Аномальные значения (выбросы) и точки влияния

«Влиятельное» наблюдение, если оно опущено, изменяет одну или больше оценок параметров модели (т.е. угловой коэффициент или свободный член). 

Выброс (наблюдение, которое противоречит большинству значений в наборе данных) может быть «влиятельным» наблюдением и может хорошо обнаруживаться визуально, при осмотре двумерной диаграммы рассеяния или графика остатков.

И для выбросов, и для «влиятельных» наблюдений (точек) используют модели, как с их включением, так и без них, обращают внимание на изменение оценки (коэффициентов регрессии). При проведении анализа не стоит отбрасывать выбросы или точки влияния автоматически, поскольку простое игнорирование может повлиять на полученные результаты

Всегда изучайте причины появления этих выбросов и анализируйте их

При проведении анализа не стоит отбрасывать выбросы или точки влияния автоматически, поскольку простое игнорирование может повлиять на полученные результаты. Всегда изучайте причины появления этих выбросов и анализируйте их.

Условные средние. Линии регрессии.

Условным средним называется среднее арифметическое наблюдаемых значений величины Y, вычисленное при условии, что величина Х приняла конкретное фиксированное значение х.

Условным средним называется среднее арифметическое наблюдаемых значений величины Х, вычисленное при условии, что величина Y приняла конкретное фиксированное значение у.

Уравнение, связывающее наблюдаемые значения величины Х и условную среднюю величины Y, называется уравнением регрессии Y на Х:

.

Уравнение, связывающее наблюдаемые значения величины Y и условную среднюю величины Х, называется уравнением регрессии Х на Y:

.

Линии на координатной плоскости, соответствующие уравнениям регрессии называются линиями регрессии.

Корреляционные зависимости могут выражаться уравнениями регрессии различных видов: линейной, параболической, гиперболической, показательной и т.д.

Гребневая (ридж) регрессия

В случае высокой коллинеарности переменных стандартная линейная и полиномиальная регрессии становятся неэффективными. Коллинеарность — это отношение независимых переменных, близкое к линейному. Наличие высокой коллинеарности можно определить несколькими путями:

• Коэффициент регрессии не важен, несмотря на то, что, теоретически, переменная должна иметь высокую корреляцию с Y.
• При добавлении или удалении переменной из матрицы X, коэффициент регрессии сильно изменяется.
• Переменные матрицы X имеют высокие попарные корреляции (посмотрите корреляционную матрицу).

Сначала можно посмотреть на функцию оптимизации стандартной линейной регрессии для лучшего понимания того, как может помочь гребневая регрессия:

min || Xw — y ||²

Где X — это матрица переменных, w — веса, y — достоверные данные. Гребневая регрессия — это корректирующая мера для снижения коллинеарности среди предикторных переменных в регрессионной модели. Коллинеарность — это явление, в котором одна переменная во множественной регрессионной модели может быть предсказано линейно, исходя из остальных свойств со значительной степенью точности. Таким образом, из-за высокой корреляции переменных, конечная регрессионная модель сведена к минимальным пределам приближенного значения, то есть она обладает высокой дисперсией.

Гребневая регрессия добавляет небольшой фактор квадратичного смещения для уменьшения дисперсии:

min || Xw — y ||² + z|| w ||²

Такой фактор смещения выводит коэффициенты переменных из строгих ограничений, вводя в модель небольшое смещение, но при этом значительно снижая дисперсию.

Несколько важных пунктов о гребневой регрессии:

• Допущения данной регрессии такие же, как и в методе наименьших квадратов, кроме того факта, что нормальное распределение в гребневой регрессии не предполагается.
• Это уменьшает значение коэффициентов, оставляя их ненулевыми, что предполагает отсутствие отбора признаков.

Корреляционный момент и коэффициент корреляции.

Мерой корреляционной зависимости двух случайных величин Х и Y служит корреляционный момент (или ковариация), который вычисляется по формуле:

, (4.1)

где средние значения (здесь и в дальнейшем предполагается, что каждая пара значений (х_i,y_i) наблюдалась по одному разу):

, , . (4.2)

Если случайные величины Х и Y независимы, то для них m_xy=0.

Из определения корреляционного момента следует, что его размерность равна произведению размерностей изучаемых величин, Это означает, что значение корреляционного момента двух величин зависит от выбора единиц измерения этих величин. Поэтому для оценки связи величин вводится другая величина, независящая от размерности измеряемых величин и называемая коэффициентом корреляции.

Коэффициентом корреляции двух измеряемых величин Х и Y называется величина:

, (4.3)

где s_х и s_у – стандартные отклонения соответственно величин Х и Y.

Поскольку размерность корреляционного момента равна произведению размерностей величин Х и Y, а стандартные отклонения имеют размерности этих величин, то коэффициент корреляции является безразмерной величиной, и поэтому он не зависит от выбора единиц измерения изучаемых величин.

Свойства коэффициента корреляции:

1) Если две случайные величины Х и Y независимы, то их коэффициент корреляции равен нулю, т.е. r = 0.

2) Модуль коэффициента корреляции не превышает единицы, т.е. |r|£1, что эквивалентно двойному неравенству: -1£r£1.

Коэффициент корреляции, вычисленный по данным выборки, называется выборочным и обозначается r_в.

Регрессия в математике

В математических науках регрессия применяется как относительная величина, отражающая зависимость среднего показателя какой-то величины от другой или нескольких величин. Такой может быть «множественная регрессия».

Линейной регрессией называют статистическую модель, отражающую зависимость одной переменной у от различных факторов – одного или нескольких. Такие факторы – независимые переменные – называются регрессорами. Через линейную регрессию можно восстановить зависимость между двумя любыми переменными.

В математических расчетах также применяются другие типы регрессий: одномерная, полиномиальная, логистическая, множественная.

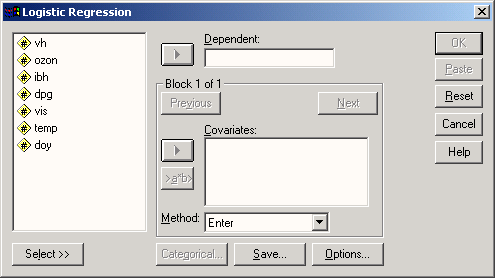
Логистическая регрессия рассматривает случаи связей между разными двумя классами, позволяет вывести обоснования и минимизировать эмпирический риск. Этот метод применяется в так называемой байесовской классификации, в методах настройки весов.

При помощи логистической регрессии (она же логит-регрессия, логит-модель) предсказывают степень вероятности наступления разных событий. Результат подгоняется к логистической кривой с использованием полученных модельных данных.

Регрессия в психологии

В психоанализе применяется термин «регрессия», где таким образом маркируют возврат от более высокой ступени психологической организации к низкой. Например, в ходе психоаналитической сессии пациент может вернуться к предыдущим этапам своего эмоционального, сексуального развития, к более примитивным и упрощенным вариантам поведения, мышления, реагирования.

Регрессией называют и сам процесс движения психики пациента в новый формат. Иногда регрессия необходима как один из этапов преодоления комплексов, зависимости, раскрытия причин психотравм и душевных ран. Это необходимо для адаптации человека к переменам во внутреннем мире и внешней среде.

Психологическая регрессия может сопровождаться необычными фантазиями, детскими и примитивными желаниями. В регрессивной форме может проявляться либидо, отношение к родителям.

Человек возвращается на прошедшую стадию развития, чтобы облегчить собственное состояние, перенести разные по силе переживания.