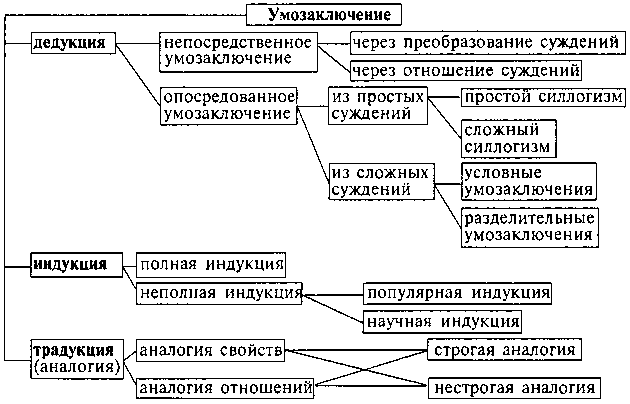
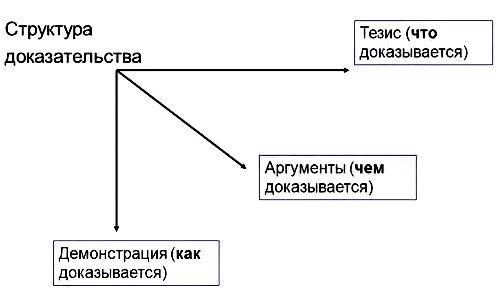
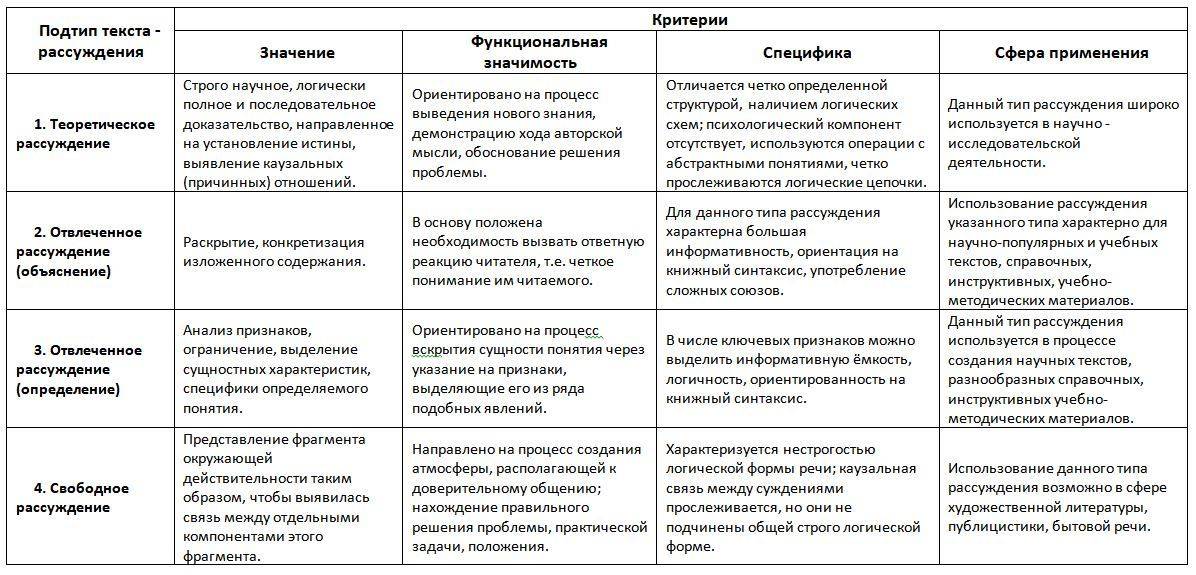
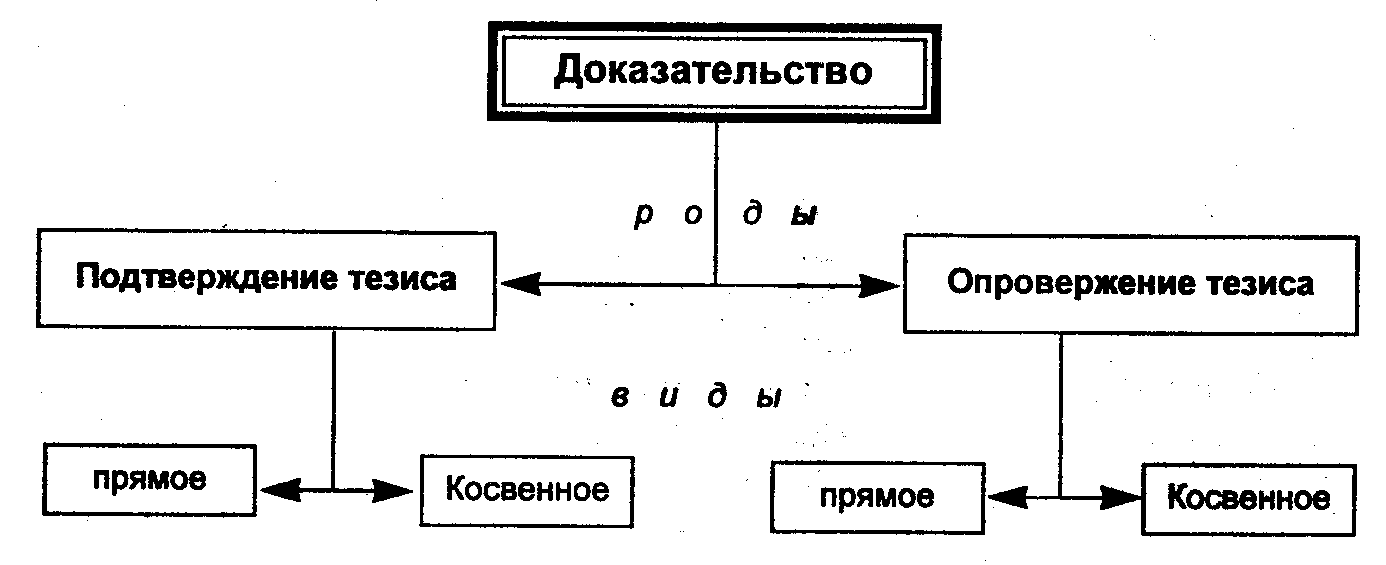
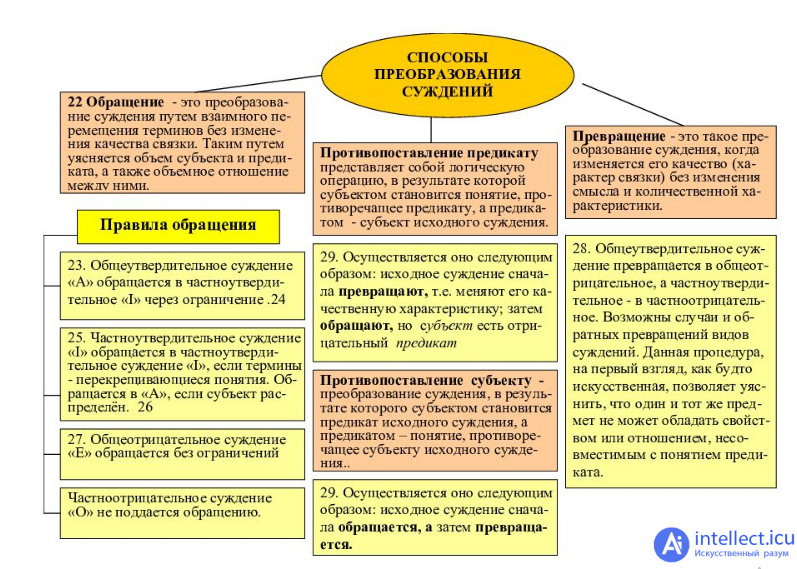
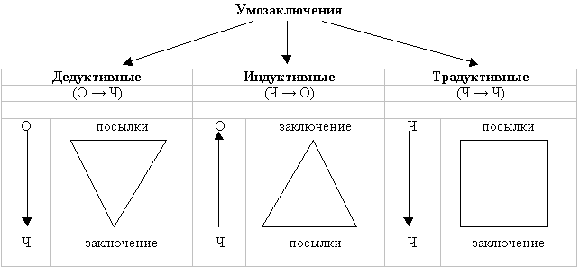
Рассуждение, его структура. характеристика умозаключения и его видов

Рассуждение, его структура. характеристика умозаключения и его видов

Прямые дедуктивные рассуждения

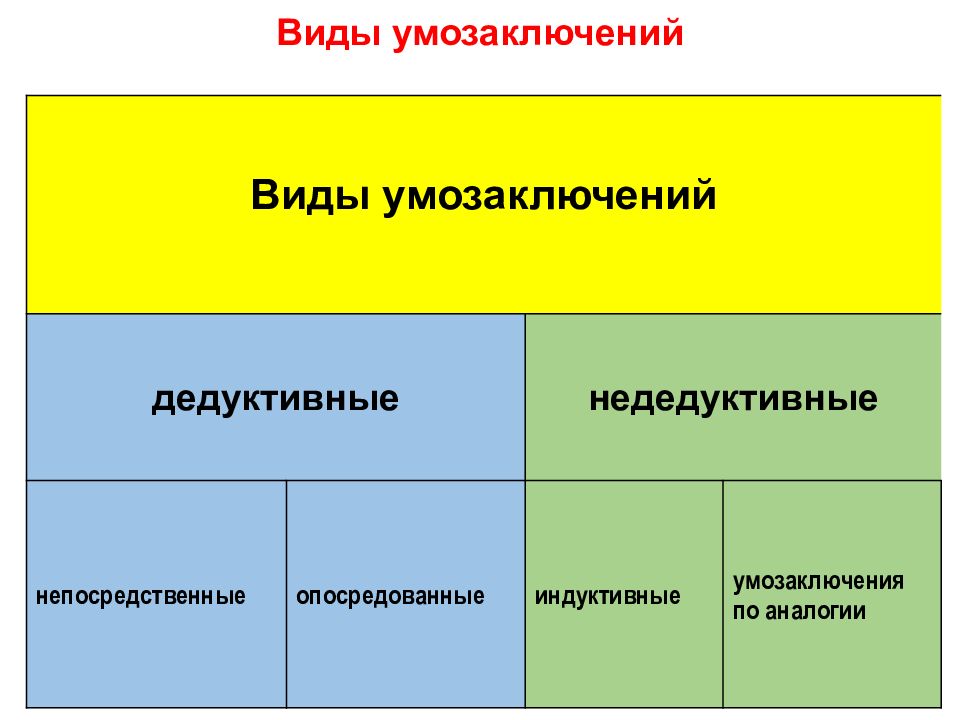
Кроме уже описанных в предыдущих уроках умозаключений из силлогистики, существует ещё несколько распространённых типов прямых дедуктивных рассуждений, о которых мы считаем полезным рассказать.

Условно-категорические умозаключения – это умозаключения, в которых одна из посылок представляет собой условное высказывание вида «Если А, то В», а вторая – простое утверждение «А» или отрицание «неверно, что В». Существует два правильных вида условно-категорических умозаключений:

Modus tollens

• Если А, то В
• Неверно, что В
• Неверно, что А

• Если число делится на 4 без остатка, то оно делится и на 2 без остатка.
• 8 делится на 4 без остатка.
• 8 делится на 2 без остатка.

• Если число делится на 4 без остатка, то оно делится и на 2 без остатка.
• 5 не делится на 2 без остатка.
• 5 не делится на 4 без остатка.

Разделительно-категорические умозаключения – умозаключения, где одна посылка представляет собой разделительное (дизъюнктивное) высказывание типа «А или В», вторая посылка – утверждение «А», «В» или отрицание «неверно, что А», «неверно, что В». Существует несколько типов правильных дизъюнктивных умозаключений.

Modus tollendo ponens

• А или В
• Неверно, что А
• В

• А или В
• Неверно, что В
• А

• «Ревизора» написал или Пушкин, или Гоголь.
• Пушкин не писал «Ревизора».
• Значит, «Ревизора» написал Гоголь

• Юля читает книги или смотрит телевизор.
• Юля не смотрит телевизор.
• Следовательно, Юля читает книги.

Отметим, что modus tollendo ponens будет правильным независимо от того, является ли разделительная посылка строгой или нестрогой дизъюнкцией.

К разделительно-категорическим умозаключениям также относится modus ponendo tollens, однако он корректен только при строгой дизъюнкции:

• Либо А, либо В
• А
• Неверно, что В

• Либо А, либо В
• В
• Неверно, что А

• Света купила либо красное платье, либо бирюзовое.
• Света купила красное платье.
• Тогда Света не покупала бирюзового платья.

• Петя либо приходит на работу в офис, либо работает удалённо из дома.
• Петя работает удалённо из дома.
• Поэтому Петя не ходит на работу в офис

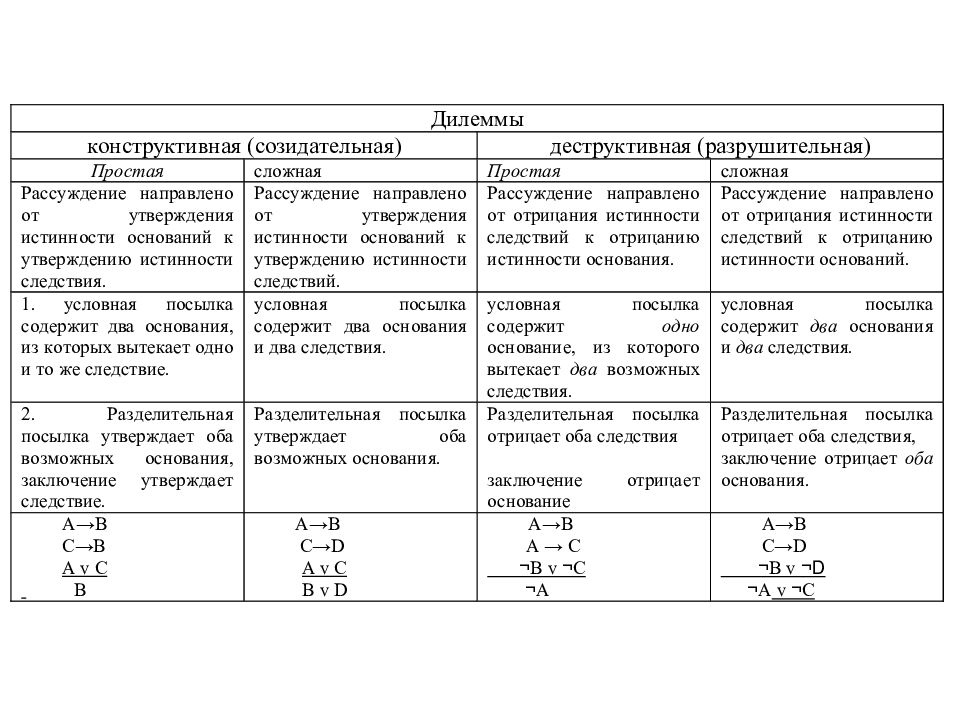
Условно-разделительные умозаключения представляют собой умозаключения, содержащие несколько условных и одну разделительную посылку. В зависимости от количества разделительных посылок, выделяют разные типы условно-разделительных умозаключений. Если умозаключение содержит две разделительные посылки, то его называют дилеммой, если три – трилеммой, но в принципе разделительных посылок может быть и больше. Мы рассмотрим только дилеммы.

Простая конструктивная дилемма

• Если А, то С
• Если В, то С
• А или В
• С

• Если Маргарита обладает привлекательной внешностью, то у неё хорошие шансы выйти замуж.
• Если Маргарита получила большое наследство, то у неё также есть хорошие шансы выйти замуж.
• Маргарита обладает привлекательной внешностью, либо она получила большое наследство.
• Маргарита имеет хорошие шансы выйти замуж.

Сложная конструктивная дилемма

• Если А, то С
• Если В, то D
• А или В
• С или D

• Если Илья Муромец пойдёт направо, то он потеряет голову.
• Если Илья Муромец пойдёт налево, то он потеряет коня.
• Илья Муромец пойдёт направо или налево.
• Следовательно, он потеряет голову или коня.

Простая деструктивная дилемма

• Если С, то А
• Если С, то В
• Неверно, что А, или неверно, что В
• Неверно, что С

• Если Толик глуп, то он вложит всё своё состояние в денежную пирамиду.
• Если Толик глуп, то он перепишет свою квартиру на мошенников.
• Толик никогда не вложит всё своё состояние в денежную пирамиду и не перепишет свою квартиру на мошенников.
• Значит, Толик не глуп.

Сложная деструктивная дилемма

• Если С, то А
• Если D, то В
• Неверно, что А, или неверно, что В
• Неверно, что С, или неверно, что D

• Если Виктор дал верные показания, то убийцей должна быть Алина.
• Если Сергей дал верные показания, то убийцей должен быть Антон.
• Либо Алина, либо Антон не является убийцей.
• Поэтому либо Виктор, либо Сергей дал ложные показания.

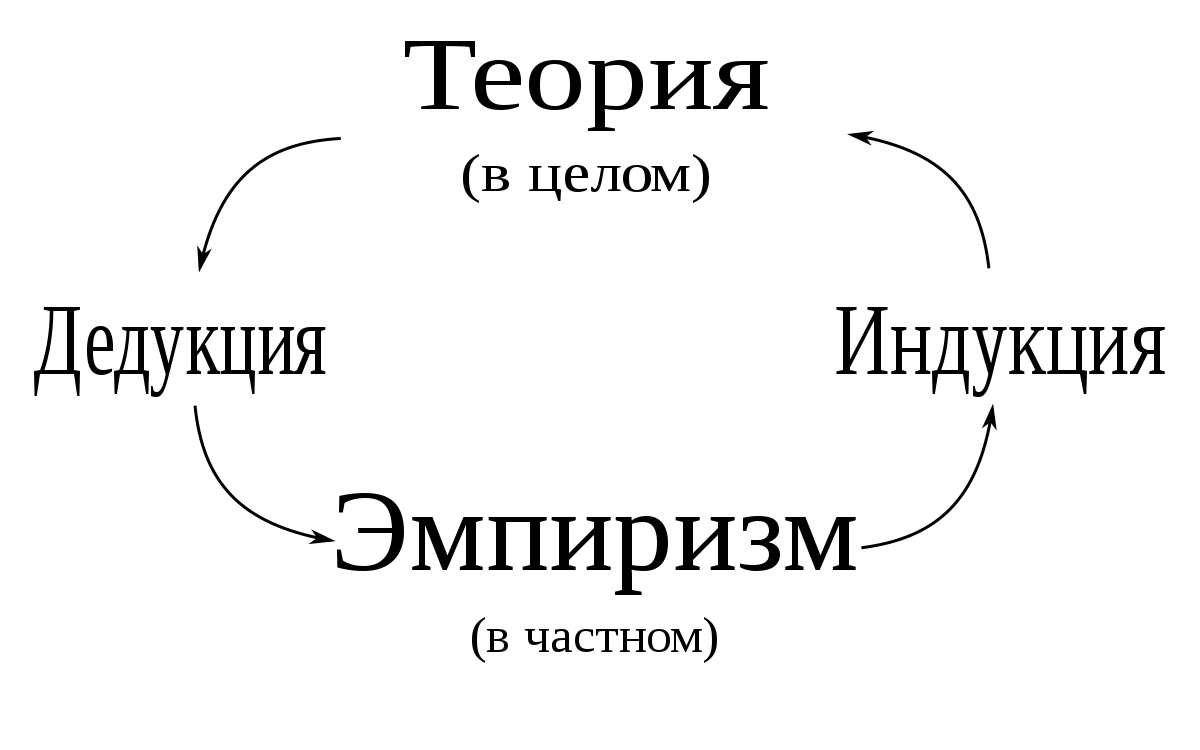
Дедукция

Только что было сказано, что дедукция характеризуется наличием строгого логического следования между посылками и заключением. Что это означает? Прежде всего, нужно сказать, что это формальное отношение – в том смысле, что оно относится к логическим формам посылок и заключения. Логики выявили, что существуют такие комбинации логических форм посылок и заключения, когда при логической истинности посылок невозможно, чтобы заключение оказалось ложным. Это и было названо отношением логического следования

Важно помнить, что в данном случае речь идёт именно о логической, а не фактической истинности высказываний. Мы уже сталкивались с логическим следованием на примере правильных модусов силлогизмов

Модус первой фигуры Barbara является правильным вне зависимости от того, что именно мы подставим на место субъекта, предиката и среднего термина, то есть в нём посылки и заключение связаны отношением логического следования. Другое дело, если мы берём ложные посылки, то, конечно, и заключение будет ложным, но сам модус в этом не виноват: при фактической истинности посылок он всегда гарантирует истинность заключения, просто благодаря определённой комбинации входящих в него логических форм высказываний.

Далее, дедуктивные рассуждения в свою очередь могут быть прямыми и непрямыми. Опять же все рассмотренные нами умозаключения представляли собой примеры прямого способа построения дедукции. Прямые дедуктивные построения строятся таким образом, что мы непосредственно переходим от посылок к заключению. Практически все разновидности простых базовых умозаключений являются прямыми. Однако в более сложных случаях непосредственный переход от посылок к заключению не всегда возможен, поэтому приходится прибегать к различным приёмам, которые косвенным образом всё же позволяют обосновать тезис с помощью имеющихся аргументов.

Аналогия

Аналогия – это такой тип рассуждения, в ходе которого в силу сходства двух предметов А и В, заключают о том, что предмет В должен обладать такими же характеристиками, что и А.

К примеру, возьмём племя тумба-юмба. Известно, что перед тем, как стать полноценным членом племени, каждый должен пройти обряд инициации, состоящий из множества испытаний. Теперь возьмём общество студентов какого-нибудь российского вуза. Во многом оно похоже на племя тумба-юмба: оно тоже устроено иерархически, есть молодняк (младшекурсники) и старейшины (пятикурсники, аспиранты), есть вождь (ректор), есть законы (устав) и т.д. Поэтому можно по аналогии предположить, что студенты российского вуза тоже должны проходить инициацию, состоящую из множества испытаний. И это действительно так: вступительные экзамены, посвящение первокурсников и т.д. Можно сказать, что наша аналогия удачна.

Рассуждения по аналогии часто встречаются как в науке, так и в повседневной жизни. Зачастую они, и правда, помогают прояснить какие-то важные вещи, могут выступать как хорошие эвристические приёмы. Однако не стоит увлекаться аналогиями: далеко не всегда они корректны. В частности, в племени тумба-юмба могут быть распространены жертвоприношения, но при всей схожести с устройством сообщества студентов, нет оснований полагать, что студенты тоже занимаются чем-то подобным.

Итак, мы рассмотрели основные типы рассуждений. По большому счёту, если вы знаете, как правильно ими пользоваться, то вы отлично вооружены практически для любой дискуссии и можете без страха пускаться в различные мыслительные построения. Конечно, мы не описали все возможные методы и способы рассуждений, например, мы полностью оставили за рамками повествования тему статистической индукции или гипотетико-дедуктивные рассуждения. Дело в том, что они тесно связаны с конкретными областями научного знания, и их абстрактные описания вряд ли имеют смысл. Также на теме рассуждений мы и завершаем наш курс. Естественно, логика простирается гораздо дальше тех тем, которые были здесь описаны. Мы выбрали только те разделы, которые наиболее полезны и легко применимы в каждодневных ситуациях. Мы надеемся, что, несмотря на это ограничение, уроки всё же помогли вам научиться мыслить и рассуждать логично. 

А теперь проверьте свое понимание рассуждений в нашем кейсе.

Cтатистика На весь экран

Непрямые дедуктивные рассуждения

Как уже было сказано непрямые дедуктивные рассуждения, или способы аргументации, задействуются, когда непосредственный переход от имеющихся посылок к заключению невозможен. Это не означает, что посылки и заключение не связаны логически: здесь также невозможна ситуация, когда посылки истинные, а заключение ложно. Просто прямое рассуждение представляет собой очень трудоёмкую задачу. Существует несколько основных способов непрямых дедуктивных рассуждений.

Рассуждение от противного должно быть многим знакомо со школьных уроков геометрии. Строится оно следующим образом: у нас есть тезис, который мы не можем доказать с помощью прямой дедукции, поэтому в качестве исходной посылки берётся его отрицание, далее из этого отрицания дедуктивно выводятся следствия, и на определённом шаге мы приходим к противоречию, то есть, например, на пятом шаге мы имеем высказывание «А», а на десятом – «неверно, что А». Как известно, логика не терпит противоречий, следовательно, можно сделать вывод, что отрицание нашего исходного тезиса было ложным, а сам тезис истинным. Что и требовалось доказать!

Сведение к абсурду очень похоже на рассуждение от противного.  Разница состоит лишь в том, что теперь мы хотим доказать ложность некоторого тезиса, а не его истинность. Поэтому в качестве исходной посылки мы берём его утверждение, а не отрицание. Опять же в ходе рассуждения на определённом шаге мы приходим к противоречию, поэтому исходный тезис не может быть истинным, а его отрицание было правильным.

Перебор случаев используется, когда нужно вывести некоторый тезис D из дизъюнктивной посылки «А или В или С». В этой ситуации можно сначала вывести D или А, потом вывести D из В, наконец вывести D из С. Если мы можем доказать, что D выводим из А, В и С по отдельности, то на основании этого перебора можно заключить, что D следует из «А или В или С». Нужно отметить, что метод перебора удобен в том случае, если количество альтернатив не очень большое: две, три, четыре. Если их больше, то лучше попробовать поискать другой метод доказательства.

Понятие

Понятие как форма мышления позволяет познавать суть предметов и явлений, устанавливать связи между ними, определять отношения объектов по отношению друг к другу, обобщать признаки.

Оно существует в виде слов, которые могут обозначать что-то единичное (один предмет – «Марс», «Тихий океан»), общее («Здание», «Человек»), конкретное («Стол», «Ложка»), абстрактное («Милосердие», «Вечность»)

Важно понимать, что понятие отражает существенные свойства предметов, объектов, явлений

Примеры подобного: треугольник можно отличить от других геометрических фигур по наличию у него трех углов (хотя у него есть и другие признаки – длина, площадь и т. д.), а животное обладает такими признаками, по которым его можно отличить от человека или растений.

Понятие как форма мышления общего характера является результатом процесса уяснения общих свойств на основе единичных предметов. Это происходит благодаря приобретению новых знаний. Формирование понятий – это всегда движение к общему от частного. Такой процесс носит название «обобщение», и оно является предметом изучения в некоторых отделах психологии (общей, возрастной, клинической).

В основе процесса усвоения понятий лежит практический опыт – если происходит его нехватка, понятия могут принимать искаженный вид, сужаться или расширяться. Это часто происходит у детей дошкольного и в некоторой степени младшего школьного возраста. К примеру, насекомые для них не являются животными, а паук – это как раз насекомое. Нарушение усвоения понятий у взрослых – это характерный признак сниженного интеллекта (умственной отсталости).

Понятие как форма мышления не идентично восприятию и представлениям памяти: оно обладает абстрактным и обобщенным характером.