Тренировка по теме «Логические выражения и таблица истинности»
№1.
Найдите значения логических выражений:
1) F= (0 /\ 0) \/ (1\/ 1)
2) F= (1 \/1) \/ (1 /\ 0)
3) F= (0 /\ 0) \/ (1 \/ 1)
4) F= ¬1\/ (1 /\ 1) \/ (¬0/\ 1)
5) F= (¬1/\ 1) \/ (1 /\ ¬1) /\ (¬1\/ 0)
№2.
Определите, истинно или ложно составное высказывание:
1)А= (2 * 2 = 4 \/ 3 * 3 = 10) /\ (2 * 2 = 5 /\ 3 * 3 = 9)
2)А = (2 * 2 = 4 \/ 3 * 3 = 10) => (2 * 2 = 5 /\ 3 * 3 = 9)
3)А= (2 * 2 = 4 /\ 3 * 3 = 10) \/ (2 * 2 = 5 \/ 3 * 3 = 9)
4)А= (2 * 2 = 4 /\ 3 * 3 = 10) <=> (2 * 2 = 5 \/ 3 * 3 = 9)
№3.
Постройте таблицы истинности для следующих формул:
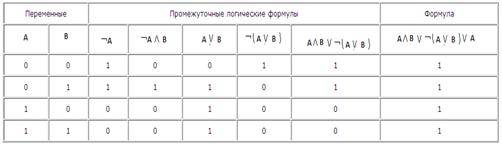
1)A/\B \/ ¬(A\/B)\/B
2)X → (Y →Z)
№4.
Выберите составное высказывание, имеющее ту же таблицу истинности, что и выражение не (не A и не(B и C)).
1)A и B или C и A;
2)(A или B) и (A или C);
3)A и (B или C);
4)A или (не B или не C)
№5.
Определите значение логического выражения: ¬ (X>Z) /\ ¬ (X=Z) , если
1) Х= 3, Z=2;
2) Х= 5, Z=-8;
3) Х= 9, Z=9.
№6.
Дан фрагмент таблицы истинности выражения F:
|
X |
Y |
Z |
F |
|
0 |
1 |
0 |
0 |
|
1 |
1 |
0 |
1 |
|
1 |
0 |
1 |
0 |
Какое выражение соответствует F?
1) ¬X\/ Y \/ ¬Z
2) X /\ Y /\ ¬Z
3) ¬X /\ ¬Y /\ Z
4) X \/ ¬Y \/ Z
№7.
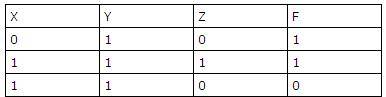
Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z. Дан фрагмент таблицы истинности выражения F:
|
X |
Y |
Z |
F |
|
1 |
0 |
0 |
1 |
|
0 |
0 |
0 |
1 |
|
1 |
0 |
1 |
0 |
Какое выражение соответствует F?
1)¬X/\¬Y/\¬Z 2) X/\Y/\Z
3) X\/Y\/Z 4) ¬X \/ ¬Y\/¬Z
№8.
Заполните пустые клетки в таблице истинности:
|
A |
B |
¬B |
A \/ B |
¬(A \/ B) |
¬B/\¬(A \/ B) |
|
1 |
0 |
||||
|
0 |
0 |
0 |
0 |
||
|
1 |
1 |
0 |
|||
|
1 |
0 |
1 |
0 |
№9.
Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: А, В, С.
Дан фрагмент таблицы истинности выражения F:
|
X |
Y |
Z |
F |
|
0 |
0 |
0 |
1 |
|
1 |
1 |
1 |
0 |
|
0 |
1 |
1 |
1 |
Чему равно F?
1) X ∧ Y ∨ Z
2) ¬X ∨ ¬Y ∨ Z
3) (X ∨ Y) ∧ ¬Z
4) ¬(X ∨ Y) → Z
Ответы:
 МИР ЛОГИКИ
МИР ЛОГИКИ